Класифікація математичних моделей

Математична модель (ММ) технічного об'єкта – це сукупність математичних об'єктів (чисел, змінних, матриць, множин і т.п.) і відносин між ними, що адекватно відбивають властивості технічного об'єкта, що цікавлять проектувальника, який розробляє цей об'єкт.

Виконання проектних операцій і процедур засноване на оперуванні ММ. З їх допомогою прогнозуються і оцінюються можливості запропонованих варіантів схем і конструкцій, перевіряється їх відповідність пропонованим вимогам, проводиться оптимізація параметрів, розробляється технічна документація і т.п.

Для кожного ієрархічного рівня сформульовані основні положення математичного моделювання, обраний і розвинутий відповідний математичний апарат, отримані типові ММ елементів проектованих об'єктів, формалізовані методи одержання і аналізу математичних моделей систем.

Складність задач моделювання і суперечливість вимог високої точності, повноти і малої трудомісткості аналізу обумовлюють доцільність компромісного задоволення цих вимог за допомогою відповідного вибору моделей. Це приводить до розширення множини використовуваних моделей і розвитку алгоритмів адаптивного моделювання.

Більш докладно зупинимося на побудові математичних моделей світлотехнічних пристроїв і електричних апаратів.

З урахуванням однієї з важливих особливостей для розглянутих об'єктів – відсутності досить строгих аналітичних залежностей між основними функціональними характеристиками і параметрами конструкції, такого класу, як наприклад, в електромагнітних пристроях, представляється безліч задач, що зустрічаються в практиці досліджень, розробки і виробництва апаратів захисту, віднести до однієї з двох груп – ідентифікації (аналізу) і оптимізації (синтезу).

Поряд з ними важливе значення має група задач обробки інформації, що виникають на будь-якій стадії створення електричного апарата. У задачах ідентифікації займаються відносинами між різними сторонами поводження об'єкта дослідження, що дозволяє на базі пізнаних співвідношень виконувати функцію пророкування.

Ідентифікація припускає встановлення якісних і кількісних взаємозв'язків між параметрами об'єкта і середовища на основі використання відомої математичної моделі або в процесі її побудови за допомогою реалізації вхідних і вихідних сигналів на об'єкті дослідження. Інакше кажучи, розв’язання задач ідентифікації дозволяє відповісти на запитання, якими будуть функціональні характеристики апарата при заданих вхідних параметрах конструкції і умовах середовища. Якщо для опису фізичного процесу є математична модель, задача ідентифікації вирішується досить просто чисельним експериментом на комп'ютері.

Прикладами таких моделей можуть служити відомі залежності переддугового W_перед і повного джоулевого W_д інтегралів, енергії дуги Е_дуг:

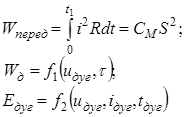(2.3)
при заданих u_дуг=f₂(t), а також співвідношення, що побудовані на основі закону теплопровідності Фур'є для провідників простої геометричної форми і законів електричного кола Ома, Кірхгофа та ін.

Відсутність адекватної математичної моделі призводить до необхідності вирішувати задачі ідентифікації на основі попередньої побудови моделі чи паралельно з побудовою моделі, що істотно ускладнює завдання.

Побудова моделі містить у собі дві основні процедури – вибір структури моделі і наближення параметрів моделі до експериментальних чи теоретичних даних. При виборі структури моделі доцільно орієнтуватися на три підходи. У загальному випадку і особливо при нових розробках для математичного опису електричних, термодинамічних, механічних та інших явищ і процесів в апаратах побудову моделі найкраще починати з вибору її структури на базі використання основних фізичних законів (наприклад, законів Ньютона, Максвелла, Кірхгофа, Фур'є, законів збереження енергії, маси, імпульсу і т.д.), тобто в їх найбільш частому, простому і фундаментальному вигляді. Прикладом може служити вигорання енергії електричної дуги плавкого елемента запобіжника. Залежність напруги на дузі U_дуг від кількості рядів перешийок у плавкому елементі запобіжника чи пластин у деіоній решітці вимикача має вигляд:

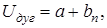(2.4)
де a, b – константи в залежності джоулева інтеграла W_д від n:

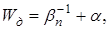(2.5)
де α і β – константи.

Математичний опис може ґрунтуватися на використанні не тільки різного роду диференціального, інтегрального, різницевого та інших рівнянь, але також на звертанні до інших видів математичних засобів – мереж і графів, блок-схем, матриць зв'язку, різних інтерполяційних рядів Тейлора, Лягерра, Чебишева та ін.

Другий підхід виходить з ідеї «чорного ящика» - кібернетичної моделі, що припускає відсутність будь якої апріорної інформації про об'єкт і реалізованої на чисто математичній основі. В абсолютній більшості технічних задач, що зустрічаються в практиці світлотехніки, припущення про те, що якийсь об'єкт чи процес є «чорним ящиком», тобто що про нього нічого не відомо, здається нереалістичним.

Нарешті, в третьому, але далеко не останньому за важливістю підході слід використовувати абстрактні ідеалізовані моделі як засіб ідентифікації, коли несуттєві для аналізу особливості ситуації відкидаються і вихідна складна задача зводиться до ідеалізованої задачі, що легко піддається математичному аналізу. Саме такий підхід привів до появи в класичній прикладній механіці і математиці блоків без тертя, нев'язких рідин, математичного маятника; аналогічні функції в перетворювальній техніці стали виконувати ідеальні вентилі, оптимізація дуги запобіжників і автоматичних вимикачів та ін.

Крім того, існують ще дискретні моделі. Найчастіше для реалізації цих моделей використовується МКР (метод кінцевих різниць) і МКЕ (метод кінцевих елементів).

Дата добавления: 2014-01-07