Характеристики форми розподілу. Через різноманітність статистичних сукупностей є багато різних форм співвідношення частот і значень варіюючої ознаки

Через різноманітність статистичних сукупностей є багато різних форм співвідношення частот і значень варіюючої ознаки.

За своєю формою розподіли поділяють на такі:

- одновершинні;

- двовершинні;

- багатовершинні.

Наявність двох і більше вершин свідчить про неоднорідність сукупності, про поєднання в ній груп із різними рівнями ознаки.

Розподіли якісно однорідних сукупностей – одновершинні. Вони поділяються на такі види:

І)- симетричні;

- асиметричні (скошені);

ІІ)- гостровершинні;

- плосковершинні.

І). У симетричному розподілі рівновіддалені від центру значення ознаки мають однакові частоти.

В асиметричному – вершина розподілу зміщена.

Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена вліво, то це правостороння асиметрія, і навпаки. Асиметрія виникає внаслідок обмеженої варіації в одному напрямку або під впливом домінуючої причини розвитку, яка веде до зміщення центру розподілу.

У симетричному розподілі характеристики центру розподілу мають однакові значення.

.

В асиметричному при правосторонній асиметрії

,

а при лівосторонній асиметрії

.

Мірою асиметрії є коефіцієнт асиметрії А, який може бути визначений як стандартизовані відхилення або через стандартизовані моменти.

Стандартизовані відхилення - відхилення між середньою арифметичною та модою чи медіаною. Вони характеризують напрям і міру скошеності розподілу та визначаються як

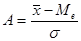або .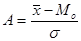

Очевидно, що у симетричному розподілі А=0, при правосторонній асиметрії А>0, при лівосторонній А<0.

ІІ) Гостровершинність розподілу відображає скупченість значень ознаки навколо середньої величини та називається ексцесом. На практиці в одному одновершинному розподілі поєднуються симетричний та гостровершинний, або скошений і плосковершинний.

Узагальнюючою характеристикою розподілу є моменти. За їх допомогою можна описати будь який розподіл.

Момент розподілу – це середня арифметична к -ступеня відхилень х-а.

Залежно від величини а моменти поділяють на такі види:

- первинні (а=0);

- центральні ();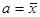

- умовні (а=const).

Ступінь к визначає порядок моменту.

Первинний момент першого порядку є середньою арифметичною 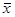, другого порядку – середній квадрат значень ознаки .

Центральний момент другого порядку характеризує варіацію , третього – асиметрію, четвертого – ексцес.

Центральні моменти та для згрупованих даних визначаються за формулами

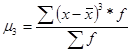та .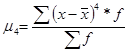

У симетричному розподілі =0. Чим більша скошеність ряду розподілу, тим більший .

Для характеристики скошеності, тобто асиметрії, використовують стандартизований момент

При правосторонній асиметрії А>0, при лівосторонній А<0. Правосторонню асиметрію через це називають додатньою, а лівосторонню – від”ємною. При А<0,25 асиметрія вважається низькою, при А<0,5 = середньою, при А>0,5 – високою.

Для вимірювання ексцесу використовують стандартизований момент четвертого порядку

.

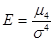У симетричному розподілі Е=3. При гостровершинному розподілі Е>3, при плосковершинному - Е<3. У цих коефіцієнтах відображається концентрація елементів сукупності.

Оцінка нерівномірності розподілу значень ознаки між окремими складовими сукупностей грунтується на порівнянні часток двох розподілів за кількістю елементів сукупності та за обсягом значень ознаки .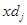

Якщо розподіл значень ознаки рівномірний, то

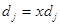
Відхилення часток свідчить про певну нерівномірність розподілу. Вона може бути виміряна за допомогою таких коефіцієнтів:

- коефіцієнт концентрації

;

.

Він є узагальнюючою характеристикою відхилення розподілу від нормального. При рівномірному розподілі К=0, при повній концентрації К=1.

Чим більший ступінь концентрації, тим більший коефіцієнт К;

- коефіцієн локалізації

.

Розраховується для кожної j -складової сукупності. При рівномірному розподілі всі . У випадку коецентрації значень у j -складовій і навпаки.

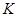і 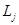- ефективний засіб вимірювання диференціації сукупності за даними інтервальних рядів з нерівними інтервалами та за даними атрибутивних рядів.

Дата добавления: 2014-01-07