Визначають середню та граничну вибіркові помилки

Середня (стандартна) помилка вибірки – це корінь квадратний з дисперсії

.

Оскільки дисперсія вибіркових помилок у n разів менша від дисперсії ознаки в генеральній сукупності, то

,

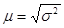і є середнім квадратичним відхиленням вибіркових оцінок від значення параметра в генеральній сукупності.

Граничний для певної ймовірності розмір вибіркової помилки становить

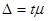
де t – квантиль нормального розподілу, який називається коефіцієнтом довіри і відповідає ймовірності Р, яку можна визначити, користуючись функцією нормального розподілу. Імовірність того, що в окремій вибірці помилка не перевищить 2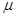, дорівнює 0,954. При Р=0,997 гранична помилка . Значення t наведені в таблиці ймовірностей розподілу помилок вибірки.

Значення t	Розподіл
Нормальний	Стьюдента
8 – 10 елементів	11 – 15 елементів
1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 3,0	0,890

На практиці при обчисленні помилки вибірки використовують дисперсію не генеральної (бо вона невідома), а вибіркової сукупності.

У великих за обсягом вибіркових сукупностях (20 і > елементів) ці дисперсії збігаються.

Якщо вибірка малочисельна, то в формулу помилки вибірки вноситься поправка 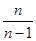. Тоді

,

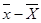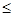
а ймовірність того, що (), визначається за таблицями розподілу Стьюдента.

У теорії вибіркового методу розглядають два способи відбору:

- повторний – здійснюється за схемою кулі, що повертається; ймовірність попасти в вибірку однакова для всіх елементів генеральної сукупності;

- безповторний – здійснюється за схемою кулі, що не повертається, ймовірність окремих елементів попасти у вибірку зростає і обсяг генеральної сукупності зменшується.

Якщо генеральна сукупність обмежена і проводиться другий спосіб, то при обчисленні помилки вибірки слід враховувати частку вибіркової сукупності в генеральній Д = . З цією метою в формулу помилки вводиться додатковий множник

Д =	0,01	0,02	0,05	0,10	0,20	0,40
	0,995	0,990	0,975	0,949	0,894	0,775

При Д 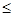0,05 наближається до одиниці і його можна не враховувати.

Отже: розмір граничної помилки вибірки середньої величини і частки обчислюється за формулами для відбору:

повторного ; (у великих за обсягом; якщо обсяг менше 30 одиниць, то n стає рівним (n-1);

безповторного

При обчисленні помилки вибірки для частки р використовують дисперсію альтернативної ознаки..

На розмір граничної помилки впливають:

1) варіація ознаки в генеральній сукупності ;

2) обсяг вибірки n;

3) частка вибірки Д = ;

4) ймовірність Р, якій відповідає квантиль t.

По-перше, чим більша варіація ознаки в генеральній сукупності, тим більша в середньому помилка вибірки. Залежність прямопропорційна.

По-друге, від обсягу вибірки залежність обернено пропорційна. Щоб зменшити помилку у 2 рази, обсяг вибірки має зрости в 4 рази.

По-третє, при безповторному відборі помилка тим помітніша, чим більша Д. Залежність пряма.

Гранична помилка вибірки для ймовірності Р – це максимальне відхилення розміру значень вибіркової оцінки від характеристики генеральної сукупності.

Можливі межі значень останьої визначають так:

- для середньої величини;

- для частки.

Дата добавления: 2014-01-07