
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Множинна кореляція і регресія
|
|
|
|
При аналізі взаємозв’язків соціально-економічних явищ, як правило, з’ясовується, які факторні ознаки впливають на результат і як з них слід включити у регресійну модель. При цьому слід пам’ятати, що всі фактори врахувати в моделі неможливо з ряду причин: частина факторів просто невідома сучасній науці, про частину відомих факторів немає достовірної інформації або кількість факторів, що включені в модель, може бути обмежена обсягом вибірки (кількість факторних ознак має бути на порядок менше чисельності досліджуваної сукупності).
Множинна регресія описує форму зв’язку у вигляді рівняння множинної регресії, або регресійної моделі (табл. 3).
Таблиця 3
Основні види множинної регресії
| Форма регресії | Вид рівняння парної регресії |
| Лінійна | 
|
| Гіперболічна | 
|
| Параболічна | 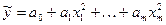
|
| Степенева | 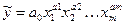
|
У таблиці позначено:
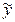 – теоретичне значення результативної ознаки (y) при певних значеннях факторних ознак (
– теоретичне значення результативної ознаки (y) при певних значеннях факторних ознак (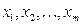 ), підставлених в регресійне рівняння;
), підставлених в регресійне рівняння;
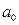 – вільний член рівняння;
– вільний член рівняння;
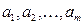 – коефіцієнти множинної регресії.
– коефіцієнти множинної регресії.
Параметри рівняння множинної регресії 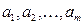 називають коефіцієнтами множинної регресії і визначають за допомогою МНК шляхом розв’язання системи нормальних рівнянь. При цьому число нормальних рівнянь у загальному випадку буде дорівнює числу параметрів. Якщо зв’язок окремого фактора з результатом не є лінійним, то проводять лінеаризацію рівняння. Для спрощення розв’язання системи нормальних рівнянь значення всіх ознак замінюють на відхилення індивідуальних значень ознак від їх середніх величин. Отримані коефіцієнти множинної регресії є іменованими числами і показують, на скільки зміниться результативна ознака (по відношенню до своєї середньої величини) при відхиленні факторної ознаки від своєї середньої на одиницю і при сталості (фіксованому рівні) інших факторів.
називають коефіцієнтами множинної регресії і визначають за допомогою МНК шляхом розв’язання системи нормальних рівнянь. При цьому число нормальних рівнянь у загальному випадку буде дорівнює числу параметрів. Якщо зв’язок окремого фактора з результатом не є лінійним, то проводять лінеаризацію рівняння. Для спрощення розв’язання системи нормальних рівнянь значення всіх ознак замінюють на відхилення індивідуальних значень ознак від їх середніх величин. Отримані коефіцієнти множинної регресії є іменованими числами і показують, на скільки зміниться результативна ознака (по відношенню до своєї середньої величини) при відхиленні факторної ознаки від своєї середньої на одиницю і при сталості (фіксованому рівні) інших факторів.
Значимість коефіцієнтів множинної регресії оцінюється на основі t-критерію Ст’юдента: 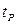 розраховують як відношення взятого за модулем коефіцієнта регресії до його середньої помилки з заданими рівнем значущості
розраховують як відношення взятого за модулем коефіцієнта регресії до його середньої помилки з заданими рівнем значущості 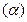 і числом степенів свободи (
і числом степенів свободи (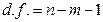 ).
).
Коефіцієнти регресії можна перетворити в порівняльні відносні показники – стандартизовані коефіцієнти регресії або β -коефіцієнти (5). β -коефіцієнт дозволяє оцінити міру впливу варіації факторної ознаки на варіацію результату при фіксованому рівні інших факторів:
 , (5)
, (5)
де 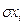 – середнє квадратичне відхилення факторної ознаки,
– середнє квадратичне відхилення факторної ознаки,
 – середнє квадратичне відхилення результативної ознаки;
– середнє квадратичне відхилення результативної ознаки;
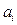 – коефіцієнт регресії при відповідному факторному ознаці
– коефіцієнт регресії при відповідному факторному ознаці 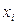 .
.
При інтерпретації результатів кореляційно-регресійного аналізу часто використовують часткові коефіцієнти еластичності ( ). Коефіцієнт еластичності (6) показує, на скільки відсотків у середньому зміниться значення результативної ознаки при зміні факторної на 1% і при сталості (фіксованому рівні) інших факторів:
). Коефіцієнт еластичності (6) показує, на скільки відсотків у середньому зміниться значення результативної ознаки при зміні факторної на 1% і при сталості (фіксованому рівні) інших факторів:
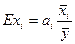 , (6)
, (6)
де 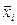 – середнє значення факторної ознаки;
– середнє значення факторної ознаки;
 – середнє значення результативної ознаки.
– середнє значення результативної ознаки.
Множинна кореляція характеризує тісноту і направленість зв’язку між результативною і кількома факторними ознаками. Основою вимірювання зв’язків є матриця парних коефіцієнтів кореляції. За нею можна в першому наближенні судити про тісноту зв’язку факторних ознак між собою і з результативною ознакою, а також здійснювати попередній відбір факторів для включення їх до рівняння регресії. При цьому не слід включати в модель фактори, що слабо корелюють з результативною ознакою і тісно пов’язані між собою. Не допускається включати в модель функціонально пов’язані між собою факторні ознаки, так як це призводить до невизначеності рішення.
Більш точну характеристику тісноти залежності дають часткові коефіцієнти кореляції. Їх зручно аналізувати, якщо вони представлені в табличному вигляді. Частковий коефіцієнт кореляції служить показником лінійного зв’язку між двома ознаками, виключаючи вплив всіх інших представлених у моделі факторів. Наприклад, для двофакторної моделі частковий коефіцієнт кореляції між y і  при фіксованому
при фіксованому  (
( ) визначається відповідно до (7).
) визначається відповідно до (7).
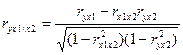 . (7)
. (7)
де 
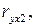
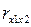 – парні коефіцієнти кореляції.
– парні коефіцієнти кореляції.
Перевірка значущості часткових коефіцієнтів кореляції аналогічна, як і для парних коефіцієнтів кореляції.
Множинний коефіцієнт кореляції (R) розраховується при наявності лінійного зв’язку між всіма ознаками регресійної моделі. Він змінюється в межах від 0 до 1. Значимість множинного коефіцієнта кореляції перевіряється на основі F-критерію Фішера. Наприклад, в двофакторній моделі при оцінці зв’язку між результативною і факторною ознаками для визначення множинного коефіцієнта кореляції можна використовувати формулу (8):

або (8)

де 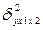 – дисперсія результативної ознаки, розрахована за регресійним рівнянням;
– дисперсія результативної ознаки, розрахована за регресійним рівнянням;
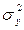 – загальна дисперсія результативної ознаки;
– загальна дисперсія результативної ознаки;

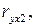
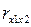 – парні коефіцієнти кореляції.
– парні коефіцієнти кореляції.
Квадрат множинного коефіцієнта кореляції називають множинним коефіцієнтом детермінації (R2). R2 оцінює частку варіації результативного фактора за рахунок представлених у моделі факторів у загальної варіації результату. Множинний коефіцієнт детермінації зазвичай коригують на втрату степенів свободи варіації за формулою (9):
 , (9)
, (9)
де  – коригуючий множинний коефіцієнт детермінації;
– коригуючий множинний коефіцієнт детермінації;
R2 – множинний коефіцієнт детермінації;
n – обсяг сукупності;
m – кількість факторних ознак.
Статистична надійність регресійного рівняння в цілому оцінюється на основі F-критерію Фішера: перевіряється нульова гіпотеза про невідповідність представлених регресійним рівняння зв’язків реально існуючим (

 ). Для перевірки
). Для перевірки 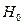 слід розрахувати значення F-критерію (
слід розрахувати значення F-критерію ( ) і порівняти його з табличним значенням (
) і порівняти його з табличним значенням ( ) із заданим рівнем значущості (
) із заданим рівнем значущості ( ) і числом степенів свободи (
) і числом степенів свободи (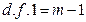 і
і  ).
).  визначається зі співвідношення факторної і залишкової дисперсії, розрахованих на одну степінь свободи за формулою (10):
визначається зі співвідношення факторної і залишкової дисперсії, розрахованих на одну степінь свободи за формулою (10):
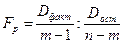 , (10)
, (10)
де 
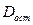 – суми квадратів відхилень, що характеризують факторну і залишкову варіації результативної ознаки.
– суми квадратів відхилень, що характеризують факторну і залишкову варіації результативної ознаки.
У разі однофакторного дисперсійного комплексу  і
і 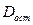 виражаються у відповідності до (11);
виражаються у відповідності до (11);
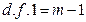 – число степенів свободи факторної дисперсії;
– число степенів свободи факторної дисперсії;
 – число ступенів свободи залишкової дисперсії.
– число ступенів свободи залишкової дисперсії.
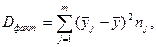
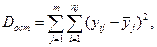 (11)
(11)
де  – значення результативної ознаки у i-ї одиниці в j-й групі;
– значення результативної ознаки у i-ї одиниці в j-й групі;
i – номер одиниці сукупності;
j – номер групи;
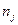 – чисельність j-ї групи;
– чисельність j-ї групи;
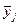 – середня величина результативної ознаки в j-й групі;
– середня величина результативної ознаки в j-й групі;
 – загальна середня результативної ознаки.
– загальна середня результативної ознаки.
Якщо  , то гіпотеза
, то гіпотеза 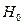 відхиляється. При цьому з ймовірністю
відхиляється. При цьому з ймовірністю 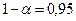 або 95%, приймається альтернативна гіпотеза про невипадкову природу оцінюваних характеристик, тобто визнається статистична значимість регресійного рівняння і його параметрів.
або 95%, приймається альтернативна гіпотеза про невипадкову природу оцінюваних характеристик, тобто визнається статистична значимість регресійного рівняння і його параметрів.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2129; Нарушение авторских прав?; Мы поможем в написании вашей работы!