Умова існування різниці, її єдиність

Мета.

Тема. Визначення різниці двох цілих невід’ємних чисел. Існування різниці, її єдиність. Операція віднімання цілих невід’ємних чисел.

План

1. Теоретико – множинний смисл різниці двох цілих невід’ємних чисел.
2. Означення різниці через суму.
3. Умова існування різниці, її єдиність.
4. Відношення «більше на», «менше на».

Ознайомити студентів із поняттям різниці двох цілих невід'ємних чисел, назвами компонентів дії віднімання, умовою існування і єдиності різниці, теоретико – множинним смислом відношень «більше на», «менше на», формувати вміння виконувати операції над скінченними множинами, застосовувати теоретичні знання при розв’язуванні прикладів і задач, розвивати мислення, виховувати інтерес до математики та обраної професії.

Література.

1. Кухар В. М., Білий Б. М. Теоретичні основи початкового курсу математики – Київ: Вища шк., 1987; Р. V, § 5.

1. Стойлова Л. П., Пышкало А. М. Основы начального курса математики: Учеб. пособие для учащихся пед. училищ – М.: Просвещение, 1988; Р. ІІ, § 8, п. 51.
2. Електронний посібник з ОПКМ; Р. ІІІ, § 6.

Студент повинен знати:

означення різниці двох цілих невід'ємних чисел як числа елементів в доповненні до множини;

означення різниці двох цілих невід'ємних чисел через суму;

назви компонентів дії віднімання;

умову існування і єдиності різниці;

теоретико – множинний смисл відношень «більше на», «менше на».

Студент повинен вміти:

виконувати операції виділення підмножини та визначення доповнення до множини;

застосовувати теоретичні знання при розв’язуванні прикладів і задач.

Основні поняття: різниця, зменшуване, від’ємник, підмножина, доповнення підмножини до множини, сума, відношення «більше на», «менше на».

1. Теоретико – множинний смисл різниці двох цілих невід’ємних чисел.

Розглянемо задачу: «В гаражі стояло 9 машин. 3 машини від’їхали. Скільки машин залишилось у гаражі?». Ця задача розв’язується виразом на віднімання: 9 − 3 = 6 (машин). Розв’язання цієї задачі пов’язано з виділенням з множини машин, які стояли у гаражі (число елементів її – 9) підмножини машин, які від’їхали (число елементів підмножини – 3) і знаходженням числа елементів у доповненні цієї підмножини, тобто множини машин, які залишились (число елементів доповнення – 6) до даної множини.

Означення. Різницею цілих невід'ємних чисел а і b називається число елементів в доповненні множини В до множини А, де n (А) = а, n (В) = b, B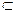A, тобто а − b = n (A\B), де n (А) = а, n (В) = b, B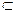A.

Різниця а – b не залежить від вибору множин, але таких, що n (А) = а, n (В) = b і B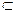A.

Приклади:

1) A = {a, b, c, d}, B = {c, d}, тобто B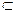A, n (A) = 4, n (B) = 2 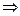A\B = {a, b}, n (A\B) = 2 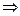4 – 2 = 2.

2) A = {Δ, Δ, Δ, Ο}, B = {Ο}, тобто B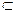A, n (A) = 5, n (B) = 1 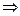A\B = { Δ, Δ, Δ }, n (A\B) = 4 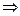5 – 1 = 4.

Дія, за допомогою якої знаходять різницю, називається відніманням. Компоненти дії віднімання – зменшуване (а) і від’ємник (b).

У початковому курсі математики ознайомлення з дією віднімання відбувається на основі практичних вправ, які пов’язані з вилученням підмножини елементів даної множини і утворенням нової множини, що є доповненням даної підмножини (без використання відповідної символіки та термінології). Основним засобом розкриття теоретико-множинного смислу віднімання є розв’язування простих текстових задач.

1. Означення різниці через суму.

Існує тісний зв’язок між додаванням і відніманням, тому правильність віднімання перевіряють додаванням.

Нехай дано цілі невід’ємні числа а і b такі, що а = n (A), b = n (B), B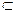A і n (A\B) = а − b. За допомогою кругів Ейлера множини A, B і A\B зображуються так:

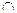Так як A = B(A\B), то n (A) = n (B(A\B)). Так як B(A\B) = , то n (A) = n (B(A\B)) = n (B) + n (A\B) = b + (а – b) = а 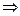різниця а – b – це таке число, яке в сумі з b дає число а. Тому маємо друге означення різниці: різницею цілих невід'ємних чисел а і b називається таке ціле невід’ємне число с, яке в сумі з числом в дає число а, тобто

а − в = c а = в + с.

Дія віднімання є оберненою до дії додавання. Дії додавання і віднімання є діями І ступеня.

Теорема про існування різниці цілих невід’ємних чисел: «Різниця цілих невід’ємних чисел а і b існує тоді і тільки тоді, коли b ≤ а».

Доведення.

1) Якщо а = b, то а – b = 0, тобто різниця а – в існує.

2) Якщо b < а, то за означенням відношення «менше» існує таке натуральне число с, що а = b + с. Тоді за означенням різниці с = а – b, тобто різниця а – b існує.

3) Якщо різниця а – b існує, то за означенням різниці існує таке ціле невід’ємне число с, що а = b + с. Якщо с = 0, то а = b; якщо с > 0, то b < а за означенням відношення «менше». Отже, b ≤ а.

Теорема про єдиність різниці цілих невід’ємних чисел: «Якщо різниця цілих невід’ємних чисел існує, то вона єдина».

Доведення. Нехай існують два значення різниці а – b: а – b = с₁ та а – b = с₂. Тоді за означенням різниці маємо а = b + с₁ та а = b + с₂. Звідси маємо в + с₁ = b + с₂, тому с₁ = с₂.

1. Відношення «більше на», «менше на».

При розв’язуванні задач та в практичній діяльності буває необхідно не тільки визначити, що число а більше (або менше) числа b, але й дізнатися на скільки число а більше (або менше) числа b.

Встановимо теоретико – множинний смисл відношень «більше на» та «менше на». Нехай а і b – цілі невід’ємні числа такі, що а = n (А), b = n (В), причому а < b. Це означає, що у множині В можна виділити власну підмножину В₁, яка рівнопотужна множині А, та множина В\В₁ не являється порожньою. Нехай n (В\В₁) = с, причому с ≠ 0. Тоді у множині В стільки ж елементів, що і у множині А. та ще с елементів. У цьому випадку кажуть, що число а менше числа b на с або число b більше числа а на с.

Так як с = n (В\В₁), де В₁ – підмножина множини В, то с = а – b.

Отже, щоб дізнатися, на скільки одне число більше або менше другого, треба від більшого числа відняти менше.

Відношення «більше на», «менше на» зустрічаються в простих текстових задачах з відношенням: це задачі на різницеве порівняння чисел, задачі на збільшення (зменшення) числа на декілька одиниць.

Задача 1: «На городі посадили 4 кущі малини та 9 кущів порічок. На скільки більше посадили кущів порічок?».

Згідно з правилом відповідь на питання задачі знаходимо за допомогою виразу на віднімання 9 – 4 = 5. Та чи можна від 9 кущів порічок відняти 4 кущі малини? Але в даному випадку від 9 кущів порічок віднімають 4 кущі порічок. Тож покажемо це, позначивши кущі малини кругами, а кущі порічок квадратами.

D

Z

Z₁

Щоб дати відповідь на питання задачі, виділимо у множині кущів порічок підмножину Z₁, рівнопотужну множині кущів малини. Тоді кущі порічок, що залишилися, утворюють доповнення множини Z₁ до множини Z та їх кількість дорівнює різниці чисел 9 і 4.

Задача 2: «На городі посадили 4 кущі малини, а кущів порічок на 5 більше. Скільки посадили кущів порічок?».

В цій задачі маємо дві множини: D – множина кущів малини, Z – множина кущів порічок. Відомо, що n (D) = 4, а кількість елементів множини Z треба знайти за умови, що в ній на 5 елементів більше, ніж у D. Тому n (Z) – n (D) = 5, звідки n (Z) = 5 + n (D) = 5 + 4 = 9.

Це також можна пояснити, спираючись на попереднє графічне зображення даних множин. Так як у множині Z на 5 елементів більше, ніж у множині D, а це означає, що у Z стільки ж елементів, скільки у D, та ще 5 елементів. Іншими словами, множину Z можна розглядати як об’єднання двох множин Z₁ і Z₂ таких, що Z₁~D та n (Z₂) = 5. Так як множини Z₁ і Z₂ не мають спільних елементів, то n (Z) = n (Z₁Z₂) = n (Z₁) + n (Z₂) = 4 + 5 = 9.

Задача 3: «На городі посадили 9 кущів порічок, а малини на 3 кущі менше. Скільки кущів малини посадили?».

В цій задачі також маємо дві множини: множину кущів порічок (Z) та множину кущів малини (D), причому n (Z) = 9, а кількість елементів множини D треба знайти за умови, що в ній на 3 елемента менше, ніж у Z. Тому n (Z) – n (D) = = 3, звідки n (D) = n (Z) – 3 = 9 – 3 = 6.

Використовуючи наступне графічне зображення, розв’язання задачі здійснюється так: оскільки кущів малини на 3 менше, ніж кущів порічок, то кущів порічок на 3 більше, тому, видаливши із множини Z підмножину з трьох елементів, отримаємо множину, рівнопотужну множині D, тобто n (D) = 9 – 3 = 6.

Z

D

Дата добавления: 2014-01-07