Правило ділення суми на число

Мета

План

Тема. Визначення поняття частки цілого невід’ємного числа і натурального через розбиття скінченної множини на еквівалентні підмножини, що попарно не перетинаються. Операція ділення на множині цілих невід’ємних чисел. Зв’язок ділення з множенням.

Мета

План

Визначення добутку двох цілих невід’ємних чисел через суму.

Тема. Визначення добутку двох цілих невід’ємних чисел як числа елементів декартового добутку двох скінченних множин.

1. Визначення добутку двох цілих невід’ємних чисел як числа елементів декартового добутку двох скінченних множин.
2. Визначення добутку двох цілих невід’ємних чисел через суму.
3. Визначення добутку декількох множників.

Ознайомити з визначенням добутку двох цілих невід’ємних чисел двома способами, встановити зв'язок з початковою школою, розширити визначення на добуток декількох множників. Розвивати вміння аналізувати, порівнювати, робити висновки. Виховувати інтерес до майбутньої професії.

Література

1. Кухар В.М., Білий Б.М. Теоретичні основи початкового курсу математики. – К.: Вища школа, 1987. Р.V § 6, с. 178-179.
2. Стойлова Л.П., Пышкало А.М. Основы начального курса математики. – М.: «Просвещение», 1988. Гл. ІІ § 8, п. 54.
3. Електронний посібник «Основи початкового курсу математики». Укл. Л.М. Голець, О.О. Кислякова, І.А. Ляшенко, О.Г. Онуфрієнко – Запоріжжя, 2010. Р. ІІІ § 7, с. 64-65.
4. Богданович М.В. Математика: Підручник для 2 кл.
5. Кочина Л.П., Листопад Н.П. Математика, 2 кл.: Підручник для середньої
   загальноосвітньої школи. - К.: Літера ЛТД.

Знати:

ü означення добутку двох цілих невід’ємних чисел через поняття декартового добутку множин;

ü означення добутку двох цілих невід’ємних чисел, в основі якого лежить поняття суми.

Вміти:

ü пояснити теоретико-множинний смисл означення добутку через суму;

ü аналізувати зміст навчального матеріалу підручників другого класу, де вводиться дія множення.

Ключові поняття: ДОБУТОК ЦІЛИХ НЕВІД’ЄМНИХ ЧИСЕЛ, ДЕКАРТОВИЙ ДОБУТОК МНОЖИН, ДІЯ МНОЖЕННЯ, МНОЖНИКИ.

1. Визначення добутку двох цілих невід’ємних чисел як числа елементів декартового добутку двох скінченних множин.

До означення добутку цілих невід’ємних чисел можна підійти через поняття декартового добутку множин. Нехай 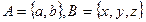. Тоді 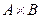складається з пар: , , ,

, , .

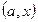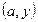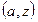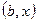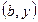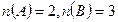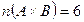, , тоді 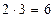. Отже, у випадку скінченних множин А і В маємо: .

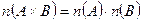Означення. Добутком цілих невід’ємних чисел а і b називається число елементів декартового добутку множини, що має а елементів, на множину, що має b елементів.

1. Визначення добутку двох цілих невід’ємних чисел через суму.

Розглянемо інший підхід до означення добутку цілих невід’ємних чисел, в основі якого лежить поняття суми.

Означення. Добутком цілих невід’ємних чисел а і b називається таке ціле невід’ємне число 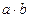, яке задовольняє такі вимоги:

1) 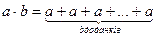, якщо ;

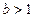2) 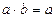, якщо ;

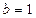3) 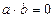, якщо .

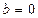Теоретико-множинний смисл цього означення наступний. Якщо множини 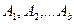містять по а елементів кожна і ніякі дві з них не перетинаються, то їх об’єднання містить 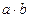елементів. Отже, добуток 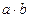- це число елементів в об’єднанні b множин, які попарно не перетинаються, кожна з яких містить по а елементів. Рівност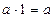і і 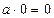приймаються за умовою, адже не можна сказати «а взяти доданком 1 раз» або «нуль раз».

Так, тільки на конкретних множинах вводять за діючими підручниками поняття добутку у другому класі. Перед учнями ставлять, наприклад, задачу: «У кожній парі по 2 вишні. Скільки всього вишень у шести парах?».

Записавши результат за допомогою суми 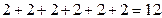(в.), з’ясовують, що такий запис суми дуже громіздкий і обчислення виконувати довго і незручно навіть при такій, порівняно невеликій, кількості доданків. А що коли б потрібно було визначити кількість вишень у 25 парах або 40? Тому умовились додавання однакових доданків вважати окремою дією – множенням – і записувати коротше: .

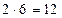Після цього поступово складають таблицю множення (тобто множення одноцифрових чисел), яку діти заучують.

Дією, за допомогою якої знаходять добуток двох чисел а і b називають множенням, числа, які перемножують, - множниками, зокрема, число а називають множеним, а число b – множником, добутком називають вираз 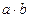і результат множення.

1. Визначення добутку декількох множників.

Розглянемо, як визначити добуток декількох множників.

Нехай добуток двох множників означено і означено добуток п множників. Тоді добуток, що складається з 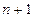множника, тобто добуток 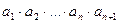, дорівнює .

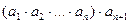Наприклад, щоб знайти добуток .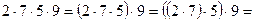

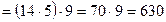1. Визначення поняття частки цілого невід’ємного числа і натурального через розбиття скінченної множини на еквівалентні підмножини, що попарно не перетинаються. Операція ділення на множині цілих невід’ємних чисел.
2. Зв’язок ділення з множенням.
3. Правила ділення.

Ознайомити з визначенням поняття частки цілого невід’ємного числа і натурального через розв’язування двох простих задач на ділення, встановити зв'язок дії ділення з дією множення. Ознайомити з правилами ділення і їх доведенням, вчити використовувати правила ділення для раціональності обчислень та розв’язування задач різними способами. Ознайомити з вивченням цих питань в початковій школі. Розвивати вміння аналізувати, порівнювати, робити висновки. Виховувати інтерес до майбутньої професії.

Література

1. Кухар В.М., Білий Б.М. Теоретичні основи початкового курсу математики. – К.: Вища школа, 1987. Р.V § 7, с. 188-191.
2. Стойлова Л.П., Пышкало А.М. Основы начального курса математики. – М.: «Просвещение», 1988. Гл. ІІ § 8, п. 56, п. 58.
3. Електронний посібник «Основи початкового курсу математики». Укл. Л.М. Голець, О.О. Кислякова, І.А. Ляшенко, О.Г. Онуфрієнко – Запоріжжя, 2010. Р. ІІІ § 7, с. 67-70.
4. Богданович М.В. Математика: Підручник для 2 кл.
5. Кочина Л.П., Листопад Н.П. Математика, 2 кл.: Підручник для середньої
   загальноосвітньої школи. - К.: Літера ЛТД.

Знати:

ü означення частки цілого невід’ємного числа і натурального;

ü в чому полягає зв'язок ділення з множенням;

ü правила ділення (окремі – з доведенням).

Вміти:

ü встановлювати зв'язок дії ділення з дією множення;

ü використовувати правила ділення для раціональності обчислень;

ü дати аналіз з навчального матеріалу підручників другого класу, де вводиться дія ділення і розкривається взаємозв’язок дій множення і ділення.

Ключові поняття: ЕКВІВАЛЕНТНІ МНОЖИНИ, ЗАДАЧІ НА ДІЛЕННЯ НА РІВНІ ЧАСТИНИ, ЗАДАЧІ НА ДІЛЕННЯ НА ВМІЩЕННЯ.

1. Визначення поняття частки цілого невід’ємного числа і натурального через розбиття скінченної множини на еквівалентні підмножини, що попарно не перетинаються. Операція ділення на множині цілих невід’ємних чисел.

Розглянемо задачі, які розв’язують учні початкової школи вже в 2 класі.

1. 10 яблук розклали на дві тарілки порівну. По скільки яблук буде в кожній тарілці?

2. Скільки треба тарілок, щоб розкласти на них 10 яблук по 2 яблука на кожну тарілку?

В обох задачах розглядається множина, що складається з десяти елементів, вона розбивається на еквівалентні підмножини, що попарно не перетинаються.

У першій задачі відома кількість цих підмножин, їх дві. Потрібно знайти кількість елементів в кожній підмножині. Задача розв’язується дією ділення:

(яблук)

і такі задачі називають «задачами на ділення на рівні частини».

У другій задачі відома кількість елементів в кожній підмножині. Потрібно знайти кількість цих підмножин. Задача розв’язується дією ділення:

(тарілок)

і такі задачі називають «задачами на ділення на вміщення».

З теоретико-множинної точки зору обидві задачі приводять до подання скінченної множини А у вигляді об’єднання еквівалентних між собою (без спільних елементів) її підмножин. Перехід до чисельної характеристики такої задачі приводить до розгляду дії ділення на множині цілих невід’ємних чисел.

Означення. Нехай і множина А розбита на еквівалентні множини без спільних елементів. Тоді, якщо b – число підмножин у розбитті множини А, то часткою чисел а і b називається число елементів кожної підмножини; якщо b – число елементів кожної підмножини в розбитті множини А, то часткою чисел а і b називається число підмножин у цьому розбитті.

Дія, за допомогою якої знаходиться частка 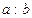, називається діленням. Числа при діленні називаються: а – ділене, b – дільник.

1. Зв’язок ділення з множенням.

Перша задача зводиться до знаходження в однакових доданків, сума яких дорівнює а:

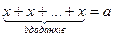, або

Друга задача зводиться до знаходження числа доданків, кожен з яких дорівнює b і сума яких а:

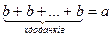, або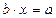

Як бачимо, в обох випадках задача зводиться до знаходження невідомого множника за відомим добутком і другим множником. Отже, ділення є дія, обернена до множення. Внаслідок її виконання знаходять частку чисел а і b.

Означення. Розділити ціле невід’ємне число а на натуральне число b означає знайти таке число с, що .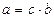

З цього означення випливає, що ділене дорівнює частці, помноженій на дільник: . З означення частки та дії ділення випливає рівність .

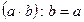1. Правила ділення.

На основі означення дії ділення та законів множення натуральних чисел неважко встановити правила ділення суми, різниці, добутку й частки на число та ділення числа на добуток і на частку.

Щоб поділити суму на число, досить поділити на це число кожний доданок і добуті результати додати: .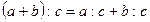

Доведення. Якщо рівність правильна, то за означенням дії ділення має бути:

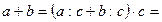(за розподільним законом множення);

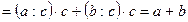(за властивістю ділення як дії, оберненої множенню).

Це правило можна поширити на будь-яке число доданків:

.

Правило ділення суми на число дуже важливе: воно є теоретичною основою алгоритму ділення багатоцифрових чисел.

У початкових класах його розкривають на конкретних задачах.

Задача. В одному сувої 12 м тканини, а в другому 15 м. з цієї тканини пошили плаття, витрачаючи на кожне по 3 м. Скільки платтів пошили?

Розв’язують задачу двома способами, дістаючи при цьому різні, але еквівалентні між собою числові формули розв’язку:

1-й спосіб 2-й спосіб

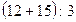
Висновок. .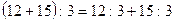

Дата добавления: 2014-01-07