Метод гармонійної лінеаризації

МЕТОДИ ДОСЛІДЖЕННЯ НЕЛІНІЙНИХ СИСТЕМ

Вони визначаються специфікою роботи нелінійних САК. Так, у них може виникати автоколивальний режим (автоколивання). Енергію для їх підтримання система одержує від зовнішніх джерел, що живлять регулятор. Період і амплітуда автоколивань визначається параметрами нелінійної САК.

До специфічних властивостей нелінійних САК відносяться:

1. Явища “м’якого” та “жорсткого” режимів збудження автоколивань. При м’якому збудженні амплітуда автоколивань плавно збільшується або зменшується при зміні параметрів системи. Жорстке збудження характеризується стрибкоподібним виникненням автоколивань при досягненні значень параметрів, що відповідають точці збудження. Жорсткому режиму властиве явище затягування автоколивань, характерне тим, що “зрив” автоколивань може здійснюватися при значеннях параметрів САК, які нижче від точки збудження, наприклад, автоколивання зникають при коефіцієнті підсилення менше критичного, не одразу, а при подальшому зменшенні його.

2. У нелінійних САК спостерігаються явища автопараметричного резонансу і “захоплення” або “ затягування” частоти. При малих значеннях різниці частот зовнішньої сили й частоти автоколивань коливальний процес вимушено синхронізується із зовнішньою частотою.

3. При подачі на вхід нелінійної системи гармонічного коливання вихідна величина може різко відрізнятися від гармонійних коливань: мати іншу частоту та амплітуду.

Ці властивості визначають необхідність розроблення спеціальних методів досліджень нелінійних систем, щоб пояснити процеси й визначити параметри вільних і вимушених коливань, здійснити аналіз та синтез.

Для дослідження нелінійних систем автоматизованого електропривода найчастіше використовують метод гармонійної лінеаризації (метод гармонійного балансу), частотний метод Попова, метод фазової площини (простору станів).

(гармонійного балансу)

Метод використовується для дослідження автоколивань (частоти, амплітуди, стійкості) в нелінійних системах високого порядку.

За кордоном цей метод називають методом описуючої функції. Цей метод наближений, але дає достатню точність дослідження параметрів автоколивань та якості перехідних процесів для нелінійних систем, що мають достатньо інерційну лінійну частину, котру можна розглядати як фільтр першої гармоніки. Він із усього спектрального складу сигналу на виході нелінійного елемента пропускає лише першу гармоніку, другу, третю та всі вищі – пригнічує (гіпотеза фільтра низьких частот). Вищі гармоніки залишаються, але малої амплітуди. Отже, нелінійна функція u = F(e) при e = А sin wt замінюється еквівалентною лінійною з точністю до вищих гармонік. Розглянемо це.

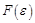
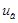
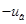
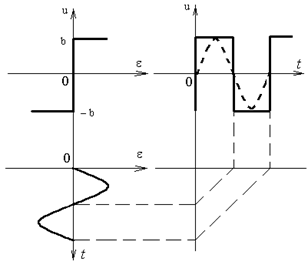
Рис. 3. Ідеальне реле

Якщо на вхід нелінійного елемента (НЕ) подається гармонійна дія , то на виході НЕ отримаємо сигнал u = F(e)=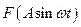, наприклад, прямокутні імпульси. Їх можна розкласти в ряд Фур’є.

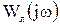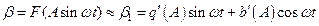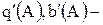Якщо лінійна частина нелінійної системи є фільтром низьких частот (ФНЧ), то на виході системи сигнал e буде дорівнювати першій гармоніці , де коефіцієнт першої гармоніки ряду Фур’є:

Це для неоднозначних (гістерезисних) симетричних нелінійностей. Для однозначних (безгістерезисних) нелінійностей .

Тому в такій САК можна розглядати, що на виході нелінійного елемента існує лише перша гармоніка сигналу, тобто u» :

де 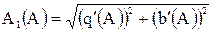– амплітуда першої гармоніки;

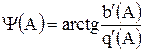– зсув фази першої гармоніки вихідного сигналу відносно вхідного сигналу e.

Запишемо комплексне зображення вхідної і вихідної (першої гармоніки) величин нелінійного елемента:

Відношення комплексних зображень першої гармоніки вихідного сигналу до вхідного називається еквівалентним комплексним коефіцієнтом підсилення нелінійного елемента (гармонічною передавальною функцією):

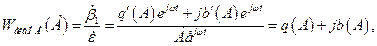
де 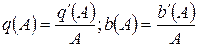– коефіцієнти гармонійної лінеаризації.

Таким чином, гармонійна лінеаризація полягає у заміні нелінійного елемента u = F(e), еквівалентним лінійним, що здійснює таке ж перетворення гармонійного вхідного сигналу, як і нелінійний елемент.

Дата добавления: 2014-01-07