Передаточної функції НЕ

Методика визначення еквівалентної комплексної

Розглянемо її на прикладі статичної характеристики ідеального реле (рис.3). При присутності на вході ідеального реле гармонійного сигналу на виході існує послідовність прямокутних імпульсів. Вихідний сигнал ідеального реле є непарною функцією (симетрія ІІ роду), а отже, коефіцієнт Фур’є 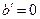, а

Еквівалентні комплексні передаточні функції інших нелінійних елементів визначаються аналогічно. Коефіцієнти гармонійної лінеаризації зведені до таблиць. Розглянемо найпоширеніші.

Таблиця коефіцієнтів гармонійної лінеаризації

Назва нелінійності	Коефіцієнти гармонійної лінеаризації
Зона нечутливості
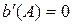
Обмеження за вихідною величиною
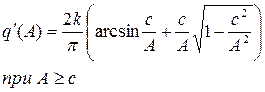
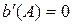
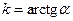
Релейна з гістерезисом
Релейна із зоною нечутливості та гістерезисом
Люфт або зазор

Як видно із таблиці, для непарних однозначних нелінійностей розкладання в ряд Фур’є не має косінусів, тому Коефіцієнт визначає гармонічну складову, що збігається за фазою з вхідним сигналом, а коефіцієнт 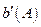– складову, що зсунуто по фазі на . Якщо нелінійність неоднозначна, то Для неоднозначних нелінійностей з від’ємним гістерезисом коефіцієнт 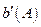від’ємний. Він визначає складову вихідного сигналу, що запізнюється за фазою на кут (при зміні знака вхідного сигналу вихідний сигнал переходить з однієї гілки статичної характеристики на іншу і тим створює запізнювання вихідного сигналу відносно вхідного.

Алгоритм дослідження нелінійних систем методом гармонічної лінеаризації

Перетворюємо алгоритмічну схему так, щоб НЕ і лінійна частина були включені послідовно.

Рис 4.

с – параметр нелінійного елемента;

А – амплітуда гармонійного коливання

Нелінійний елемент заміняється лінійним . Комплексна передавальна функція розімкненої САК тоді буде: , де – нормований параметром нелінійності (рис 4) комплексний передаточний коефіцієнт нелінійного елементу (гармонічна передаточна функція нелінійного елементу).

Припускаємо, що замкнена нелінійна система знаходиться на межі стійкості і в ній є незатухаючі коливання. Тоді відповідно до критерію Найквіста АФЧХ розімкненої системи повинна проходити через точку (-1; j0). Звідки випливає умова існування коливань у замкненій системі:

,

де – нормований множник.

або

.

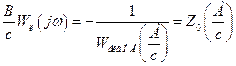Тепер у показниковій формі

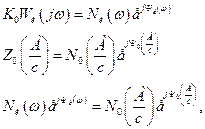
звідки випливають дві умови існування коливань у замкненій системі: коливання існують, якщо виконуються умови баланса фаз і амплітуд на одній і тій же частоті.

– умова балансу амплітуд

;

– умова балансу фаз

;

або у логарифмічній формі

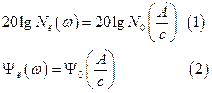
Умова (1) – виконується при перетині ЛАЧХ лінійної частини і НЕ.

Умова (2) – при перетині їх фазових характеристик.

Автоколивання можливі, якщо точка перетину амплітудних та фазових характеристик відповідає одній і тій же частоті. Вони можуть існувати у замкненій САК навіть за відсутності будь-якої вхідної дії.

Дата добавления: 2014-01-07