Методика побудови ЛЧХ нелінійного елемента

Запишемо АЧХ нелінійного елемента:

тоді ЛАЧХ нелінійного елемента має вигляд:

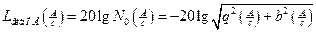. (1)

Вираз для фазової характеристики нелінійного елемента

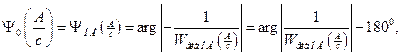
звідки

(2)

У випадку безінерційних нелінійних елементів, як випливає із (1) і (2), амплітудні й фазові логарифмічні характеристики їх не залежать від частоти і є прямими, паралельними осі абсцис.

Для визначення амплітуди й частоти автоколивань y = A sin w_at достатньо побудувати серію характеристик L(w) для різних значень А. Ці характеристики будуть паралельні одна одній.

Шуканим значенням амплітуди А буде таке, при якому на частоті зрізу Y(w_з) = – p. Для характеристик, показаних на рис.5 А = А₃; w_а = w_зз.

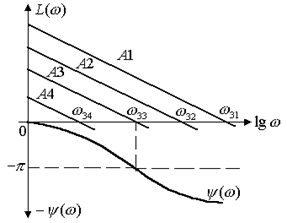
Рис.5

Умова знаходження нелінійної системи на межі стійкості при дослідженні автоколивань може використовуватися за будь-яким критерієм стійкості: Гурвіца, Михайлова, але найчастіше Найквіста.

У підсумку можна сказати, що існування автоколивального процесу в нелінійних САК характеризується рівнянням гармонійного балансу:

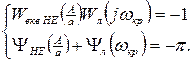
Ці рівняння дозволяють визначити параметри автоколивань і їх стійкість.

Приклад. Визначити частоту й амплітуду автоколивань нелінійної системи.

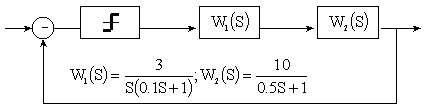
Рис.20

Розв’язок: .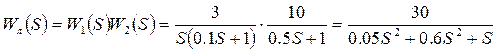

Із таблиці визначимо коефіцієнти амплітудної лінеаризації:

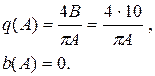
Виведемо q(A) та b(А):

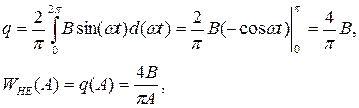
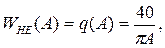
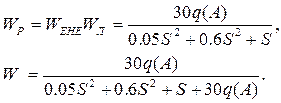
Характеристичне рівняння замкненої системи:

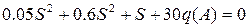– рівняння автоколивань нелінійної САК.

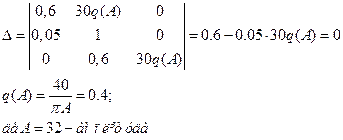
Визначимо частоту коливань. Для цього уявну частину характеристичного рівняння прирівнюємо до 0:

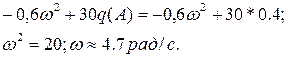
Тобто в системі існують автоколивання з частотою 4,7 рад/с і амплітудою 32.

Приклад. Методом гармонічної лінеаризації визначити амплітуду й частоту автоколивань нелінійної системи.

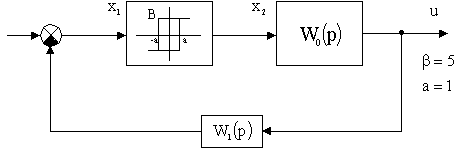
Рис.21

Розв’язок:

,

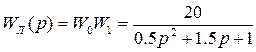Із таблиці: 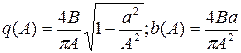, при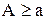

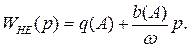
Характеристичне рівняння вільних коливань:

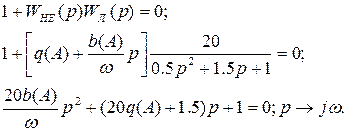
Виділимо дійсну та уявну частину характеристичного рівняння, прирівнявши їх до 0.

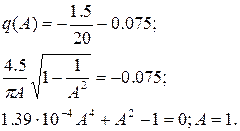
Частота:

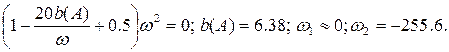
Частота від’ємна, тому автоколивань у системі не існує.

Приклад. Визначити амплітуду і частоту автоколивань нелінійної системи, характеристичне рівняння (рівняння рівного руху) якої має вигляд: .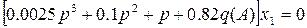

Нелінійна ланка має параметри:

;

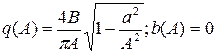В=5, а=1, збурююча дія .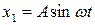

Розв’язок. Параметри автоколивань визначимо за допомогою критерію Михайлова. Для цього в характеристичному рівнянні замкненої системи підставимо 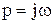і виділимо дійсну та уявну частини.

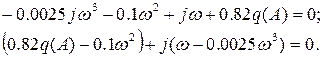
Із уявної частини визначимо частоту автоколивань.

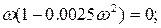
Визначимо амплітуду автоколивань із дійсної частини.

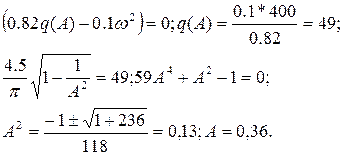
Дата добавления: 2014-01-07