Инвестиционных проектов

Лекция 21. Методы обработки экспертной информации для отбора

Смысл обработки экспертной информации (ЭИ) заключается в нахождении согласованной результирующей оценки инноваций по оценкам, данным экспертами.

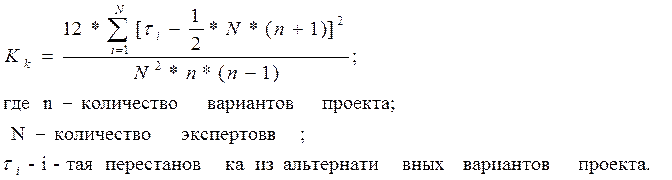
Статистические методы основаны на предположении о том, что отклонение предположений экспертов от истинных оценок происходит в силу случайных причин. Задача состоит в том, чтобы восстановить это истинное значение с наименьшей погрешностью. В этих методах результаты оценок каждого из экспертов можно рассматривать как реализацию некоторой случайной величины, принимающей значения из некоторого множества. Имеется возможность применять к множеству допустимых оценок (МДО) методы математической статистики. Статистические методы позволяют:

1) определять согласованность мнений экспертов;

2) определять значимость полученных оценок;

3) определять степень согласованности (указывает на качество результирующей оценки);

Примечание. Во всех рассматриваемых методах предполагается:

А) изолированность экспертов;

Б) отсутствие обратной связи;

В) различия в МДО (и его наличие);

Г) наличие истинной оценки (желаемое значение оценок);

(21.1)

Численные оценки. В этом методе отыскивается результирующая оценка как средневзвешенная

с учётом «весов» экспертов. Степень согласованности мнений экспертов определяется дисперсией, имеющей вид:

(21.2)

Ранжирование (строгое и нестрогое) – в этих методах задача состоит в сопоставлении параметров оцениваемого проекта (или одного показателя), одной перестановки из альтернативных вариантов, предлагаемых экспертами. В этом методе составляется таблица: по строкам откладываются N экспертов, а по столбцам – n вариантов проекта. Далее выбирается ранг оценки. Степень согласованности мнения экспертов определяется с помощью коэффициента конкордации, который характеризует степень связности комбинаторных перестановок:

	(21.2)

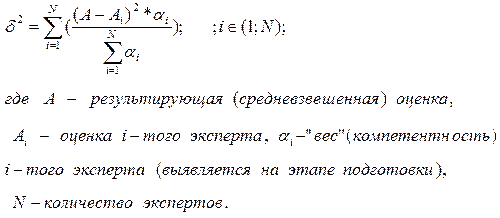
Примечание. Выражение 21.2 характерно для строгого ранжирования. Для нестрогого ранжирования коэффициент конкордации К_к определяется по более сложной формуле (слишком сложной, чтобы её здесь писать).

Алгебраический метод заключается в том, что на множестве допустимых оценок (МДО) W задаётся расстояние, и результирующая оценка определяется как та оценка, сумма расстояний от которой до оценок экспертов минимальна. Результирующая оценка А₀ имеет вид:

Причём, АєW, D- расстояние между ранжировками А и А_i.

Методы шкалирования. Заключаются в том, что по экспертной информации о степени различия проектов устанавливается минимальный или близкий к минимальному набор критериев и оценок проектов по ним, обуславливающих указанное экспертами различие. Используется в экспертизах, где требуется сопоставление попарных различий между одноимёнными параметрами проектов, из которых (различий) составляется векторный многоугольник шкал; задача состоит в том, чтобы найти результирующий вектор многоугольника, который и будет результирующей оценкой в данной шкале. В векторном многоугольнике шкал критерии задаются так, чтобы расстояния в многоугольнике были максимально близки к исходным попарным различиям.

Примечание. Если критерий обращается в нуль, то задача имеет точное решение (полное согласование мнений экспертов).

Метод простой ординации -графический метод представления многоугольника шкал, спроецированного на ось ординат, на которую проецируется попарное различие между параметрами проекта.

Метод троек заключается в разбиении многоугольника шкал, в которых сопоставляются расстояния между по парными различиями параметров проектов.

В отличие от выше рассмотренных линейные методы используются, когда не удаётся построить на МДО линейное отображение многоугольника шкал. В нелинейных методах применяют итерационные процедуры линеаризации. В каждой из итераций приближают расстояние между попарными различиями параметров проекта к различиям, заданным критериями.

Метод одномерного шкалирования содержит следующие методики:

1) вычисление матрицы ранжировок, данных экспертами, в которой элемент матрицы интерпретируют как вероятность предпочтения Р_i;

2) вычисление результирующей оценки А_i,j, исходя из таблиц нормального распределения с учётом известных вероятностей предпочтения;

3) подсчёт суммы результирующих оценок для различных вероятностей предпочтения, пронормированной в показателях относительной важности проекта;

4) проверка на непротиворечивость.

Многомерное шкалирование сводится к построению ранжировки, её нормированию и размещению результатов в вершинах правильного (n-1)-мерного многоугольника шкал, центр которого находится в начале координат (многоугольник - симплекс). Далее производится расчёт расстояний между попарными различиями параметров по известным формулам геометрии.

Дата добавления: 2014-01-07