Включение и исключение в дереве

Begin

Begin

Begin

Begin

S:= <преобразование информационных
полей элемента рNode^ в строку>;

Form1.Memo1.Lines.Append(S);

End;

Теперь можно привести тексты трех подпрограмм обхода, которые реализуют приведенные выше рекурсивные алгоритмы:

Procedure PreOrder(pRoot: Pvertex);

If (aRoot <> Nil) Then Begin

ProcessingNode(pRoot);

PreOrder(pRoot^.Left);

PreOrder(pRoot^.Right);

End;

End;

Procedure InOrder(pRoot: Pvertex);

If (aRoot <> Nil) Then Begin

InOrder(pRoot^.Left);

ProcessingNode(pRoot);

InOrder(pRoot^.Right);

End;

End;

Procedure PostOrder(pRoot: Pvertex);

If (aRoot <> Nil) Then Begin

PostOrder(pRoot^.Left);

PostOrder(pRoot^.Right);

ProcessingNode(pRoot);

End;

End;

Для активации любой из этих трех процедур, следует воспользоваться вызовом в следующем виде:

<имя процедуры>(Root);

где Root - указатель корня, например: PostOrder(Root).

9.4.4 Преобразование любого дерева к бинарному дереву

Любое m -арное дерево (т. е. дерево степени m) может быть преобразовано в эквивалентное ему бинарное дерево, которое проще исходного дерева с точки зрения представления в памяти и обработки. Графически такое преобразование сводится к следующим действиям:

1) сначала в каждом узле исходного дерева вычеркиваем все ветви, кроме самой левой ветви, которая соответствует ссылке на старшего сына;

2) в получившемся графе соединяем те узлы одного уровня, которые являются братьями в исходном дереве.

На рисунке 9.10 приведен пример такого преобразования, причем после него из некоторых элементов, исходят две ссылки: горизонтальная соединяет данный элемент с его младшим (в исходном дереве) братом, а вертикальная - с его старшим сыном. Если на рисунке 9.10 повернуть все ссылки на 45° по часовой стрелке, то получим структуру, очень похожую на двоичное дерево. Однако считать ее таковым было бы ошибкой, поскольку функционально горизонтальные и вертикальные ссылки на рисунке 9.10 б имеют совершенно разный смысл. Правильнее было бы использовать следующую интерпретацию: после выполнения указанных преобразований из сыновей каждого родителя образуется линейный список, причем на старшего сына указывает ссылка от его родителя, а сам старший сын находится в голове списка своих братьев.

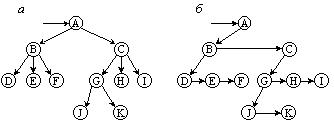
Рисунок 9.10 - Преобразование 3-арного дерева к бинарному

Пользуясь аналогичным алгоритмом можно представить в виде двоичного дерева и лес. На рисунке 9.11 показаны этапы преобразования леса из двух деревьев в бинарное дерево.

Переход от m -арного дерева (или леса) к представлению в виде двоичного дерева при естественном связном хранении сокращает объем занимаемой памяти, поскольку каждый элемент m -арного дерева должен иметь m полей для логических указателей, тогда как элемент двоичного дерева имеет только два таких поля. С другой стороны, при таком преобразовании нужно помнить о функциональном назначении левой и правой ссылок и учитывать это при обработке дерева.

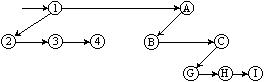
Рисунок 9.11 - Преобразование леса к бинарному дереву

Рассмотрим некоторые особенности операций включения и исключения в любом m ‑арном дереве.

9.5.1 Включение в дереве

Включаемым в дерево объектом является некоторое (другое) дерево, которое затем станет поддеревом. При выполнении операции включения должны быть заданы:

1) включаемое поддерево (т. е. в памяти должна существовать соответствующая древовидная структура),

2) та вершина исходного дерева, к которой «подвешивается» в качестве ветви включаемое дерево и

3) индекс, назначаемый поддереву и определяющий старшинство его корня среди сыновей вершины подключения.

В результате операции включения поддерева Y в вершину Х исходного дерева степень исхода вершины Х увеличивается на единицу и у этой вершины появляется еще один сын. При этом в общем случае потребуется заново перенумеровать вершины-сыновья узла X.

9.5.2 Исключение в дереве

Исключаемым объектом, применительно к произвольному дереву, является некоторое поддерево. В операции исключения следует указать вершину исходного дерева, играющую роль корня исключаемого поддерева, и номер (или индекс) исключаемого поддерева, поскольку одна вершина в зависимости от ее степени исхода может играть роль корня для разных поддеревьев.

Пусть Х - некоторая вершина произвольного дерева, а вершины, Y₁..., Y_n - ее сыновья. Тогда исключение i -ого поддерева вершины Х означает уменьшение степени исхода Х на единицу и удаление из исходного дерева ветви Х ® Y _i , и поддерева, корнем которого служит вершина Y _i. В результате такого удаления вершина Х может стать листом.

Дата добавления: 2014-01-07