Четвертая теория (энергетическая)

Она наилучшим образом согласуется с экспериментальными данными для пластичных материалов типа сталь. Утверждается, что элемент тела единичного объема разрушится тогда, когда работа максимальных касательных напряжений достигнет предельного значения.

Для трехосного напряженного состояния в разных плоскостях имеем 3 разных :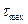

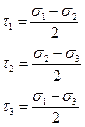
Рассмотрим работу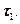

Рис.11.16

Имеем:

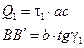
Работа силы 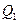на перемещении будет:

.

В виду малости угла сдвига имеем:

.

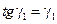Примем, что объем элемента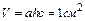

Таким образом, получаем:

.

По закону Гука (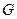- модуль сдвига):

.

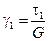Окончательно получим: .

Аналогично, максимальные касательные напряжения в других плоскостях дают работы:

, .

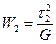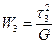Суммируя их, получим:

.

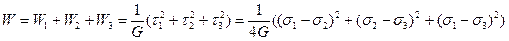Обозначим работу внутренних сил, приводящих к разрушению элемента тела, через .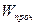

Тогда критерий разрушения можно записать в виде:

.

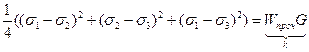Выразим правую часть через 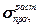. Рассмотрим частный случай - одноосное растяжение. Тогда в момент разрушения:

.

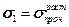
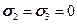Подставляя в критерий разрушения, получим:

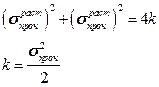
Окончательно четвертая теория теперь примет вид:

.

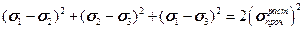Рассмотрим теперь частный случай, когда = 0, который имеет место в балках и плитах строительных сооружений. Тогда получим критерий в виде:

.

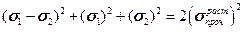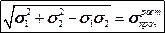или

Предельная кривая примет вид эллипса, приведенного на рис.11.15.

11.5.5. Пятая теория – критерий Мора

Формулируется для элемента тела, который растягивается в продольном направлении и сжимается в поперечном направлении (см. рис.11.18).

Рис.11.18. Рис.11.19.

Для некоторых материалов (например, для бетона) было обнаружено, что он, предварительно сжатый в поперечном направлении (см. рис.11.19), хуже работает на растяжение в продольном направлении.

Запишем это утверждение аналитически. Учтем, что при растяжении 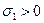, при поперечном сжатии 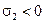. Тогда разрушение произойдет при

,

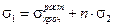где n > 0 – некоторый коэффициент. Выразим n через пределы прочности материала.

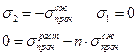Для этого сначала рассмотрим разрушение при простом сжатии. Тогда получим:

Отсюда: .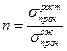

Таким образом, для элемента тела, который растягивается в продольном направлении и сжимается в поперечном направлении получим критерий Мора в виде:

.

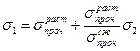В 1-ой и 3-ей четвертях (т.е. при растяжении или сжатии в обоих направлениях) применяют первую теорию. Предельная кривая примет вид многоугольника, приведенный на рис.11.20.

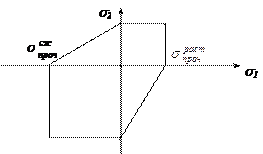Рис.11.20

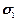
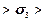
Примечание. Если на элемент тела кроме действует еще , при этом , а также 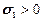, , 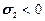то критерий Мора записывают так же

.

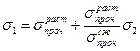Это означает, что влиянием на прочность элемента пренебрегают.

Дата добавления: 2014-01-07