
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нормальные напряжения. Формула Навье
|
|
|
|
Рассмотрим элемент изогнутой балки (рис. 15.1-15.2)
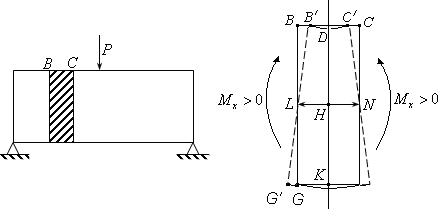
рис.15.1 рис. 15.2
Здесь 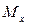 - момент внешних сил, которые воздействуют на наше сечение слева или справа (по определению он называется изгибающим моментом).
- момент внешних сил, которые воздействуют на наше сечение слева или справа (по определению он называется изгибающим моментом).
Ясно, что верхние волокна сжимаются (например, ВС), а нижние - растягиваются. Между ними есть волокно LN, которое не деформируется (рис.15.2). Очевидно, что чем дальше волокна от LN, тем больше удлинение волокон, значит по закону Гука и сила их растяжения больше. Таким образом, максимальное напряжение будет там, где волокна наиболее удалены от 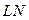 .
.
Для вывода формулы вычисления напряжений используем метод сечений. Рассмотрим поперечное сечение DК (рис.15.2, 15.3)). Проведем ось х через точку Н (рис 15.3). На этой линии, напряжений не будет.
Определение: Линия HR, на которой нет напряжений, называется нейтральной.
Таким образом, ось 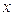 будет лежать на нейтральной линии, так как на ней
будет лежать на нейтральной линии, так как на ней 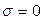 (для удобства записи индексы для напряжений σz, τzy в дальнейшем будем опускать).
(для удобства записи индексы для напряжений σz, τzy в дальнейшем будем опускать).
На верхнюю часть нашего элемента правая часть балки действует сжимающим напряжением 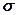 , а на нижнюю - растягивающим (см.рис.15.3).
, а на нижнюю - растягивающим (см.рис.15.3).
Разобьем сечение на малые микроплощадки dA. Рассмотрим одну из них. На неё с правой стороны действует следующая сжимающая сила:
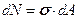 (15.1)
(15.1)
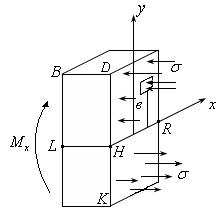 рис. 15.3
рис. 15.3
| Относительно оси 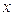 сила сила 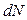 имеет плечо имеет плечо 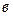 , следовательно, , следовательно, 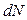 создаёт момент:
dM = в dN (15.2)
Из рисунка видно, что плечо в - это координата центра микроплощадки создаёт момент:
dM = в dN (15.2)
Из рисунка видно, что плечо в - это координата центра микроплощадки 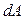 . Значит в = у. Тогда: . Значит в = у. Тогда:
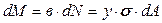 (15.3) (15.3)
|
Суммируя, получаем результирующий момент, который создают напряжения 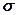 :
:
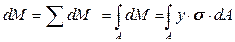 (15.4)
(15.4)
Поскольку вся балка находится в покое, то и любой его элемент тоже статичен. Следовательно, можно записать уравнение статики и для элемента, изображенного на рис.15.3. Запишем его в виде:
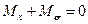 .
.
Отсюда:
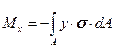 (15.5)
(15.5)
Для отыскания 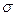 из (15.5) учтем, что чем дальше микроплощадка от
из (15.5) учтем, что чем дальше микроплощадка от 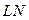 , тем больше
, тем больше 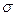 . То есть, чем больше в, тем больше
. То есть, чем больше в, тем больше 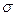 . Учитывая, что в = у, эту фразу можно записать в виде:
. Учитывая, что в = у, эту фразу можно записать в виде:
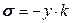 (15.6)
(15.6)
Здесь 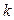 - коэффициент пропорциональности, а знак «-» поставлен потому, что при
- коэффициент пропорциональности, а знак «-» поставлен потому, что при 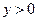 (т.е. в верхней части) действуют сжимающие напряжения.
(т.е. в верхней части) действуют сжимающие напряжения.
Примечание. Соотношение (15.6) можно считать первым членом разложения функции σ в ряд Маклорена по аргументу у.
Найдем 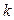 (если известен
(если известен 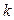 , то будем знать формулу для
, то будем знать формулу для 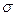 ).
).
Подставим 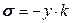 в (15.5), тогда:
в (15.5), тогда:
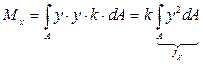 (15.7)
(15.7)
Согласно определению 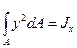 - это момент инерции сечения. Таким образом,
- это момент инерции сечения. Таким образом,
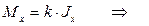
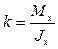 .
.
Окончательно формула для 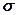 принимает вид:
принимает вид:
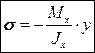 (15.8)
(15.8)
Здесь у - это координата точки (микроплощадки 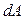 ), в которой вычисляется напряжение,
), в которой вычисляется напряжение, 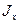 -осевой момент инерции. Формулу (15.8) нередко называют формулой Навье.
-осевой момент инерции. Формулу (15.8) нередко называют формулой Навье.
Примечание. Согласно закону Гука по формуле (15.6) получим, что 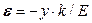 . Это означает, что линия GG ′ - прямая. Эксперимент подтверждает этот вывод для длинных балок. Тогда, можно пойти дальше и считать, что сечение со следом ВG остается плоским. Это предположение называют гипотезой Бернулли. Его обычно принимают за исходное положение. Тогда формула (15.6) будет следствием гипотезы Бернулли.
. Это означает, что линия GG ′ - прямая. Эксперимент подтверждает этот вывод для длинных балок. Тогда, можно пойти дальше и считать, что сечение со следом ВG остается плоским. Это предположение называют гипотезой Бернулли. Его обычно принимают за исходное положение. Тогда формула (15.6) будет следствием гипотезы Бернулли.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 3547; Нарушение авторских прав?; Мы поможем в написании вашей работы!