Стержней замкнутого профиля

Напряжения при свободном кручении тонкостенных

Рассмотрим тонкостенный стержень с замкнутым профилем (рис.18.19)

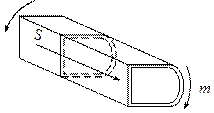
рис.18.19

Введем систему координат 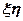, где ось 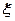проходит по точкам, которые делят стенку пополам (рис.18.20). В общем случае толщина t стенки может быть разной при разных 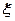, т.е.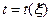

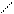
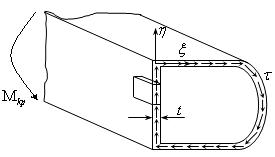
рис.18.20 рис.18.21

Рассмотрим задачу вычисления . Ввиду тонкостенности можно считать, что напряжения 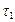, 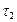не изменяются по толщине, но могут быть разными при разных ξ. Вырежем элемент стержня (см. рис.18.20, рис.18.21). В силу закона парности на верхней грани действует 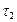, а на нижней .

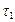Запишем уравнение равновесия в виде равенства нулю суммы сил на продольную ось S.

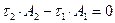
Поскольку: 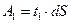, , 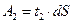то:

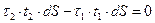
Таким образом,

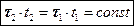(18.14)

Выразим через внешние моменты. Рассмотрим сечение, приведенное на рис.18.22.

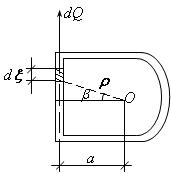
рис.18.22

Сила 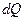- это равнодействующая напряжений , действующих на площадку 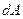длиной :

.

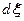Эта сила создает момент около точки О:

.

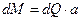Найдем сумму всех dM:

.

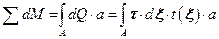Из условия равновесия левой части стержня (см.рис.18.20) вытекает, что

.

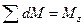Учтем, что 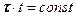согласно (18.14). Эту константу можно вынести:

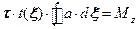(18.16)

Найдем геометрический смысл подынтегрального выражения. Рассмотрим нашу площадку (рис.18.23). Из рисунка видно, что площадь треугольника BDO равна 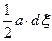, т.е.

. (18.17)

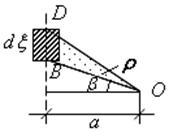
рис.18.23 рис.18.24

Интеграл – это сумма таких площадей. Таким образом, получим, что интеграл равен удвоенной площади фигуры, которая ограничена штриховой линией, изображенной на рис.18.25.

(18.18)

Определение: Эту площадь А^* назовем площадью просвета трубы.

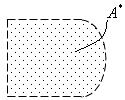
рис.18.25

Подставляя (18.18) в (18.16) видим, что:

.

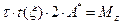Отсюда вытекает формула Бредта:

. (18.19)

Из (18.19) следует, что при кручении труб разрушение начинается там, где толщина стенки минимальна.

Дата добавления: 2014-01-07