Прямая линия, пересекающая плоскость

Алгоритм решения задачи на построение точки пересечения прямой линии с плоскостью является весьма важным среди других позиционных задач начертательной геометрии. Этот алгоритм используется также для решения задач на построение точек пересечения прямых с поверхностью, поверхности с плоскостью, взаимного пересечения линейчатых поверхностей.

Рассмотрим алгоритм решения задачи на построение точки пересечения прямой с плоскостью на пространственной модели.

Пусть плоскость общего положения Q пересекается прямой с EF (рис. 4.10). В этом случае точка пересечения прямой с плоскостью определяется с помощью вспомогательной плоскости. Для упрощения построений вспомогательная плоскость обычно берется проецирующей.

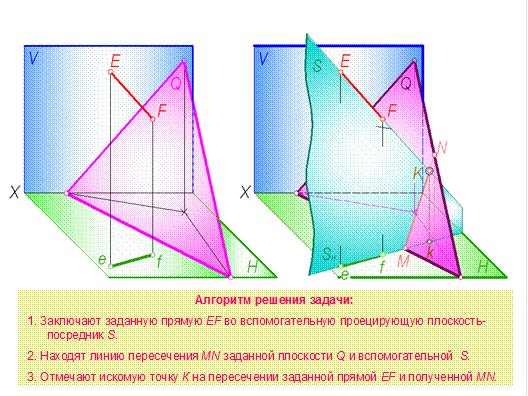
Рис. 4.10

Алгоритм решения состоит из трех операций.

1. Заключают заданную прямую EF во вспомогательную проецирующую плоскость-посредник S.

2. Находят линию пересечения заданной плоскости Q и вспомогательной S. На слайде видно, что эти плоскости пересекаются по линии MN.

3. Отмечают искомую точку K на пересечении заданной прямой EF и полученной MN.

На рис. 4.11 показано решение аналогичной задачи на метрическом эпюре.

Рис. 4.11

В качестве вспомогательной плоскости использована фронтально проецирующая плоскость S, проведенная через прямую EF.

Найдена линия пересечения двух плоскостей – отрезок I-II. Последовательность построения показана на рисунке стрелками.

На пересечении горизонтальных проекций прямых ef и 12 отмечена горизонтальная проекция искомой точки k, фронтальная проекция которой определяется по проекционной связи.

Определим видимость прямой относительно плоскостей проекций, применяя способ так называемых конкурирующих точек.

Конкурирующими называют точки, лежащие на одном проецирующем луче.

Если смотреть по направлению проецирующего луча, то можно увидеть ту из конкурирующих точек, которая наиболее удалена от плоскости проекций (или, что то же самое, наиболее близко расположена к нам).

Так на горизонтально-проецирующем луче III-IV находятся точки 33′ и 44′, принадлежащие прямым EF и CD. Точка 33′ принадлежит прямой EF, а точка 44′ стороне CD четырехугольника.

По фронтальным проекциям 3′ и 4′ этих точек устанавливаем, что одна из них (точка 44′) расположена выше другой (точка 33′) относительно плоскости проекций H. Следовательно, на участке KIII прямая линия EF (если смотреть на горизонтальную плоскость проекций H) находится под плоскостью ABCD, т.е. закрыта четырехугольником. Поэтому условно горизонтальную проекцию прямой на участке k3 покажем штриховой линией.

Чтобы определить видимость прямой относительно фронтальной плоскости проекций, воспользуемся фронтально проецирующим лучом I-V. Здесь точка 11′ принадлежит стороне AD четырехугольника, а точка 55′ – прямой EF. По местоположению горизонтальных проекций этих точек устанавливаем, что точка I ближе к нам, чем точка V.

Поэтому на участке K-V (если смотреть на фронтальную плоскость проекций V) прямая EF закрыта плоскостью ABCD и является невидимой. Условно на участке k′5′ фронтальную проекцию e′f′ прямой покажем штриховой линией.

Если один из элементов пересечения –плоскость или прямая - проецирующие, то использовать рассмотренный алгоритм не рекомендуется, так как в большинстве таких случаев нахождение точки пересечения значительно упрощается.

На рис. 4.12 показано построение точки K пересечения горизонтально проецирующей прямой EF с плоскостью общего положения ABC. Горизонтальная проекция k точки K совпадает с проекцией ef, а фронтальная проекция k′ легко определяется из условия принадлежности точки K плоскости ABC, для чего использована вспомогательная прямая A-I, принадлежащая плоскости ABC.

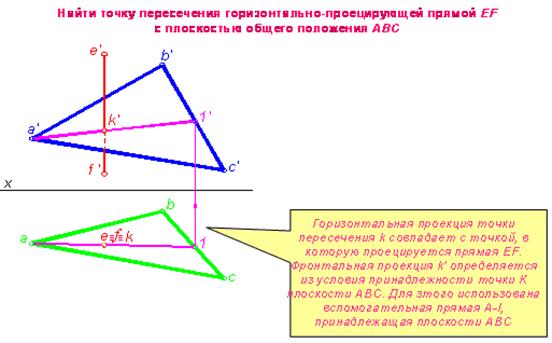
Рис. 4.12

4.2.3. Прямая линия перпендикулярна плоскости

Прямая перпендикулярна плоскости, если ее проекции перпендикулярны одноименным следам плоскости или соответствующим проекциям горизонтали и фронтали (рис. 4.13 и 4.14).

Прямой угол между перпендикуляром к плоскости и горизонталью, проходящей через его основание, проецируется на плоскость Н в виде прямого угла, как угол, одна из сторон которого параллельна плоскости Н. Аналогично прямой угол между перпендикуляром и фронталью, проецируется на плоскость V в виде прямого угла.

На эпюре (рис. 4.6) показано построение проекций прямой, проведенной через точку D (d, d′) перпендикулярно к плоскости, заданной треугольником ABC (abc, a'b'c'). Для определения положения проекций перпендикуляра в плоскости треугольника проведены горизонталь и фронталь.

На эпюре (рис. 4.7) показано такое же построение в случае, когда плоскость задана следами Р_Н и Р_V. Для определения положения проекций перпендикуляра здесь служат следы плоскости.

Рис. 4.13 Рис. 4.14

Таким образом, если прямая перпендикулярна двум пересекающимся прямым, принадлежащим плоскости, то она перпендикулярна самой плоскости.

Данное условие позволяет решать ряд задач начертательной геометрии: опустить или восстановить перпендикуляр к плоскости, решить обратную задачу – провести плоскость перпендикулярно прямой и определить расстояние от точки до плоскости.

Задача 1. Определить расстояние от точки А до плоскости треугольника BCD.

Проведем в плоскости треугольника BCD (рис. 4.15) горизонталь В1 (b1; b ¢ 1 ¢) и фронталь С2 (с2; с ¢ 2 ¢) и опустим из точки а¢ перпендикуляр на прямую с ¢ 2 ¢, а из точки а - перпендикуляр на прямую b1. Основанием перпендикуляра является точка его пересечения с плоскостью BCD. Для того, чтобы найти точку пересечения перпендикуляра с плоскостью заключаем перпендикуляр в горизонтально проецирующую плоскость R, которая пересекает плоскость треугольника BCD по прямой MN (mn; m ' n'). На пересечении m ' n' с фронтальной проекцией перпендикуляра находим фронтальную проекцию его основания - точку k¢. Спроецировав точку k¢ на горизонтальную проекцию линии MN (mn), получим точку k. Натуральную величину перпендикуляра АК определим способом прямoугольного треугольника как длину гипотенузы A ₀ k ¢треугольника A ₀ a ¢ k ¢.

Рис. 4.15

Задача 2. Определить расстояние от точки А до плоскости Р, заданной следами.

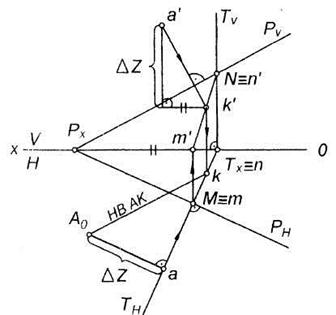
Строим проекции перпендикуляра к плоскости. Горизонтальную проекцию перпендикуляра проводим из точки а перпендикулярно горизонтальному следу плоскости P_H, а фронтальную проекцию из точки а ¢ перпендикулярно P_V (рис. 4.16). Основанием перпендикуляра является точка его пересечения с плоскостью P. Чтобы ее найти, заключаем перпендикуляр в горизонтально проецирующую плоскость T, которая пересекает плоскость Р по прямой MN (mn; m ¢ n'). На пересечении фронтальной проекции прямой с фрон-тальной проекцией перпендикуляра находим фронтальную проекцию его основания – точку k¢. Спроецировав точку k¢ на горизонтальную проекцию линии MN (mn), получим точку k. Натуральную величину перпендикуляра АК определим способом прямoугольного треугольника.

Рис. 4.16

Дата добавления: 2014-01-07