Прямых и плоскостей

Позиционные задачи на взаимное расположение

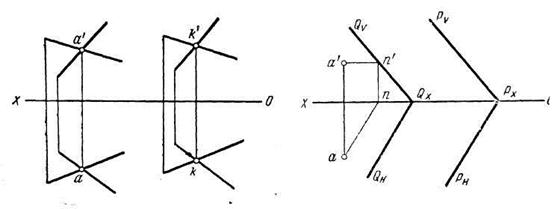
Задача 1. Через точку А провести плоскость Q, параллельную заданной плоскости Р.

Рис. 4.17 Рис. 4.18

Если плоскость задана пересекающимися прямыми (рис. 4.17), то решение задачи сводится к проведению через точку А пары прямых, параллельных заданным.

Если плоскость задана следами (4.18), то построение может быть выполнено по следующему алгоритму:

1. Через точку А проводим, например, горизонталь искомой плоскости Q, параллельную горизонталям заданной плоскости Р.

2. Через эту горизонталь проводим искомую плоскость параллельно заданной. Фронтальный след Q_V проводим через фронтальную проекцию п' фронтального следа горизонтали параллельно следу P_V; горизонтальный след Q_H - через точку Q_Х параллельно следу Р_Н.

Задача 2. Через точку А (а, а') провести плоскость Q, перпендикулярную к прямой (рис. 4.19).

а) Требуется показать искомую плоскость пересекающимися прямыми. В этом случае наиболее просто построить плоскость Q главными линиями — горизонталью и фронталью, проходящими через точку А (а, а').

Рис. 4.19 Рис. 4.20

б) Требуется показать искомую плоскость следами. Построение может быть выполнено по следующему алгоритму. Через точку А проводим горизонталь плоскости Q перпендикулярно к отрезку ВС. Затем через эту горизонталь проводим искомую плоскость перпендикулярно к прямой ВС. Фронтальный след Q_V проводим через фронтальную проекцию п' фронтального следа горизонтали перпендикулярно b'с′; горизонтальный след Q_H —через точку Q_Х перпендикулярно к bс.

Задача 3. Через точку А (а, а') провести плоскость Q, перпендикулярную к заданной плоскости Р и проходящую через точку схода следов Q_Х на оси X (рис. 4.20).

Известно, что плоскость Q будет перпендикулярна к заданной плоскости Р, если она проходит через перпендикуляр к ней или перпендикулярно к линии, лежащей в плоскости Р.

На рис. 4.20 решение задачи выполнено по плану, использующему первое из этих условий:

1. Через заданную точку А проведен перпендикуляр к плоскости Р (am┴P_H,, a′m′┴P_V).

2. Через этот перпендикуляр и заданную точку Q_X проведена искомая плоскость Q. При этом след Q_Н проведен через горизонтальную проекцию т горизонтального следа перпендикуляра и точку Q_X; след Q_V — через фронтальную проекцию п′ фронтального следа перпендикуляра и точку Q_X.

Искомую плоскость можно было бы построить и пересекающимися прямыми, если через точку Q_X провести какую-либо прямую, имеющую общую точку с перпендикуляром.

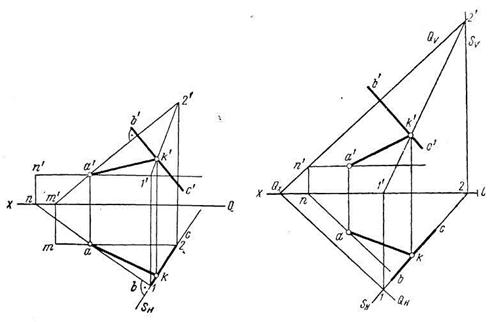
Задача 4. Через точку А (а, а') провести прямую, перпендикулярную к прямой ВС.

Искомый перпендикуляр лежит в плоскости, перпендикулярной к заданной прямой ВС. Поэтому задача может быть решена по следующему алгоритму:

1. Через точку А проводим плоскость Q, перпендикулярную к прямой ВС.

2. Определяем точку К (k, k') пересечения прямой ВС с плоскостью Q при помощи горизонтально-проецирующей плоскости S.

3. Соединяем точки А и К.

На эпюре, решая задачу по этому алгоритму, можно плоскость показать двумя пересекающимися главными линиями (h×f) (рис. 4.21) или следами (рис. 4.22).

Рис. 4.21 Рис. 4.22

Задача 5. Построить линию пересечения плоскостей ABC и DEF.

Эту задачу можно решать с использованием задачи на пересечение прямой с плоскостью. На рис. 4.23 показано построение линии пересечения плоскостей, заданных треугольниками ABC и DEF. Прямая MN построена по найденным точкам пересечения сторон DF и EF треугольника DEF с плоскостью треугольника ABC.

Например, чтобы найти точку М пересечения стороны DF с плоскостью ABC, через прямую DF проводят фронтально-проецирующую плоскость Р, которая пересекается с плоскостью треугольника ABC по прямой I II. На пересечении горизонтальных проекций df и 12 получают горизонтальную проекцию m искомой точки М. Затем находят фронтальную проекцию m ' точки М. Точку N пересечения прямой EF с плоскостью ABC находят, используя фронтально-проецирующую плоскость Q, которая пересекается с плоскостью треугольника ABC по прямой III IV. На пересечении горизонтальных проекций ef и 34 получают горизонтальную проекцию n искомой точки N.

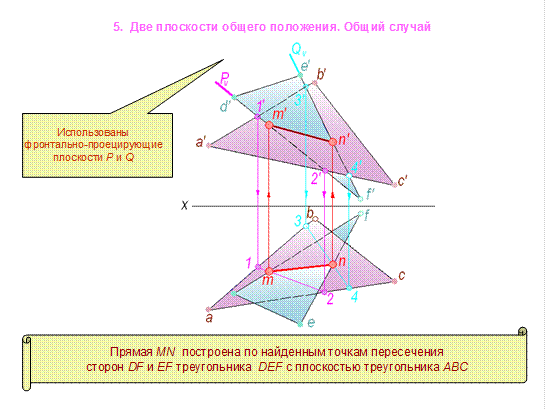
Рис. 4.23

Соединив попарно точки m ' и n ', m и n, получают проекции линии пересечения MN плоскостей ABC и DEF.

Видимость частей отрезков плоскостей устанавливается способом конкурирующих точек.

Дата добавления: 2014-01-07