Вращение вокруг проецирующих прямых

Способ вращения

Сущность способа вращения состоит в изменении положения объекта, заданного на эпюре, таким образом, чтобы определенные его элементы заняли относительно плоскостей проекций частное положение и проецировались без искажений.

Рассмотрим следующие разновидности способа вращения:

1. вращение вокруг проецирующих прямых;

2. плоскопараллельное перемещение;

3. вращение вокруг линий уровня и совмещение.

При вращении важно правильно определить его элементы: ось, а также плоскость, центр, радиус и угол вращения.

При вращении точки вокруг оси, перпендикулярной плоскости проекций, одна ее проекция перемещается по окружности, а вторая – по прямой, перпендикулярной проекции оси вращения (рис. 5.7).

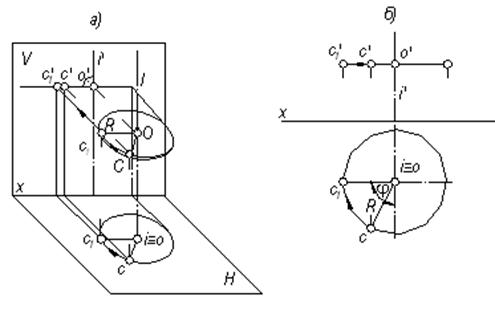
Рис. 5.7

Окружность, описываемая точкой С, проецируется на плоскость Н без искажения, а на плоскость V – в виде отрезка прямой. При вращении точки вокруг фронтально проецирующей оси ее траектория проецируется на фронтальную плоскость проекций в виде окружности, а на горизонтальную плоскость – отрезком прямой, перпендикулярным проекции оси.

Если требуется повернуть точку С на угол φ, то, откладывая этот угол на горизонтальной проекции (рис. 5.7 б), получим горизонтальную проекцию с₁, а по ней найдем фронтальную проекцию с₁′ повернутой точки С₁.

Задача 1. Определить длину отрезка прямой АВ общего положения (рис. 5.8).

Алгоритм решения задачи:

1. Проведем ось вращения I (i, i′) через точку В (b, b') перпендикулярно к плоскости Н.

2. Повернем отрезок АВ так, чтобы он стал параллелен плоскости V. При вращении точка В останется неподвижной, поэтому для решения задачи достаточно повернуть точку А в положение, при котором горизонтальная проекция а₁b расположится параллельно оси X. Тогда отрезок А₁В будет параллелен плоскости V, а его фронтальная проекция а′₁b′ будет равна длине заданного отрезка АВ.

В данной задаче одновременно найден угол α наклона отрезка прямой АВ к плоскости Н.

Рис. 5.8

Задача 2. Определить натуральную величину и форму треугольника ABC (рис.5.9).

Рис. 5.9

Первым вращением вокруг оси I₁ (i₁, i₁′), перпендикулярной к плоскости Н и проходящей через вершину В (b, b'), плоскость треугольника преобразована во фронтально-проецирующую. Для этого в плоскости треугольника проведена горизонталь BD (bd, b'd'), которая затем повернута на угол φ₁ в положение фронтально-проецирующей прямой. Второе вращение произведено на угол φ₂ вокруг оси I₂ (i₂, i₂′), проведенной через вершину С₁ (с₁, с₁) перпендикулярно к плоскости V. Построенная проекция a₂b₁с₁ определяет натуральную величину и форму треугольника ABC.

5.2.2. Способ плоскопараллельного перемещения

Сущность способа плоскопараллельного перемещения заключается в том, что все точки геометрического объекта, изменяющего свое положение в пространстве, перемещаются в плоскостях, параллельных одной из плоскостей проекций.

Прямоугольная проекция объекта на плоскость, параллельно которой происходит перемещение его точек, сохраняет свои размеры и форму, изменяя лишь положение относительно оси проекций. Проекции всех точек объекта на другой плоскости перемещаются по прямым линиям, параллельным оси проекций и являющимся следами плоскостей вращения. Такое преобразование позволяет избежать наложения проекций.

Задача 1. Найти расстояние от произвольной точки S (s, s') до плоскости треугольника ABC (рис. 5.10).

Рис. 5.10

Располагаем треугольник АВС в проецирующей плоскости, например, по отношению к плоскости V. Для этого в плоскости треугольника проводим горизонталь ВD (bd, b ¢ d ¢) и располагаем новую его горизонтальную проекцию а ₁ b ₁ с ₁, равную проекции аbс, в произвольном месте чертежа так, чтобы bd стала перпендикулярна к оси Ох. Тогда горизонталь будет перпендикулярна к плоскости V, а плоскость треугольника АВС займет положение фронтально проецирующей плоскости и спроецируется на плоскость V в отрезок прямой а ₁¢ b ₁¢ с ₁¢. Далее строим новую проекцию s ₁, сохраняя равенство расстояний b ₁ s ₁= bs и с ₁ s ₁= сs, и по ней находим фронтальную проекцию s ₁'. Отрезок перпендикуляра s ₁' е ₁ ' определяет искомое расстояние.

Обратным перемещением находим проекции расстояния в первоначальном задании.

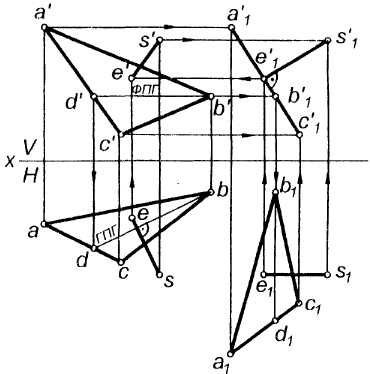
Задача 2. Определить натуральную величину и форму треугольника ABC (рис. 5.11).

Рис. 5.11

Треугольник последовательно перемещаем сначала параллельно одной, а затем параллельно другой плоскости проекций. Первым перемещением, параллельным, например, плоскости Н, располагаем плоскость треугольника перпендикулярно к плоскости V, используя горизонталь BD (bd, b^′d') (см. задачу 1). Вторым перемещением, параллельным плоскости V, располагаем треугольник параллельно плоскости Н. Новую фронтальную проекцию a₂'b₂′с₂′, равную проекции а₁′b₁′с₁′ строим параллельно оси X и получаем новую горизонтальную проекцию в виде треугольника a₂b₂c₂, равного заданному треугольнику ABC.

Дата добавления: 2014-01-07