
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Центр дистанционного образования
|
|
|
|
Общие принципы совершенствования химико-технологических процессов в технологии неорганических веществ. Оценка достоверности исходных физико-химических и технологических данных.Методы оптимизации химико-технологических процессов.
Применение каталитического метода ускорения химических превращений в технологии неорганических веществ.Виды катализа.Гомогеный и гетерогенный катализКинетика гетерогеных каталитических реакций. влияние температуры, давленя, концентрации реагентов на скорость гетерогенно-каталитических реакций.
Кинетика сложных химических процессов:обратимые, паралельные, последовательных.Стадиипротекания сложных реакций. Расчет скоростей реакций и протекания процесов. Влияние температуры и давления на скорость реакций.
Константы химического равновесия. Методы расчета констант равновесия для гомогенных и гетерогенных реакций. Факторы, влиящие на состояние равновесия: температура, давления, исходные соотношения между реагентами.
Общие условия равновесия. Термодинамические потенциалы. Характеристические функции. Химическиий потенциал. Равновесие устойчивое и неустойчивое. Физико –химические предпосылки переноса вещества и энергии.
Для того чтобы однозначно характеризовать свойства системы состояние которой определяется какими либо параметрами (P,V,T) при термодинамическом равновесии, недостаточно знать уравнение состояния этой системы, связывающее давление, обьем и температуру. Для полной характеристики нужно знать еще уравнение, которая позволяет определить энергию системы по данным параметром состояния. Анализ первого и второго начало термодинамики показывает что число уравнений, можно свести с двух до одного, поскольку все необходимые для этого величины могут быть выражены через некоторую функцию независимых переменных и ее производные.
Такие функции получили название характеристических функций. Наиболее часто в качестве таких функций используются: внутренняя энергия (U),энтальпия (H), свободная энергия (F) и термодинамический потенциал(G)
Любое свойство системы может быть выражено через эти характеристические функции (U,H,F,G) и их производные в явной форме.
Однако использование той или иной функции зависит от конкретных условий, которые диктуют нам выбор независимых переменных, а это в свою очередь определяет выбор используемой характеристической фуекции. Наиболее простые в матеематическом отношении выражения для различных свойств системы получаются, если рассматривать U как функцию отV и S:
U=f (V,S);
H как функцию от p и S:
H = f (p,S);
F как функцию от V и T:
F = f (V,T);
и G как функцию от p и T:
G = f (p,T).
При применении функций U и H одной из независимых переменных является энтропия. Невозможность непосредственно измерять энтропию представляет U и H. В зтом заключается одна из причин того, что чаще пользуются функциями F и G при удобных для измерения независимых переменных V и T или Р и Т. Вместе с тем нельзя пользоваться во всех случаях только одной из этих функций. Например, если мы попытаемся использовать функцию F в случае, когда по условиям опыта надо взять в качестве независимых переменных p и T, то функция F не будет характеристической и даст выраженииие для ряда свойств системы в неявной форме. Следовательно, для данного случая необходимо воспользоваться функцией G.
Внутреняя энергия
В соответствии с уравнением U=f (V,S);внутреняя энергия является характеристической функцией при независимых переменных V и S.
Как и в случае всякой другой функции состояния, дифференциал функции U является полным дифференциалом и, следовательно, может быть представлен как сумма частных дифференциалов по независимым переменным:


Воспользовавшись уравнением первого начало термодинамики  где dA =pdV, и уравнением второго начало термодинамики dQ =TdS, получаем
где dA =pdV, и уравнением второго начало термодинамики dQ =TdS, получаем
TdS = dU +pdV,
Откуда
dU=TdS –pdV
Сравнивая уравнения видим, что

 v = T и
v = T и 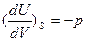 .
.
Таким образом, зная что U=f (V,S);, легко получаем значенм\ия недостающих переменных Т и р. Причем становится очевидным, что температура является мерой возрастания внутренней энергии системы с увеличением энтропии при постоянном обьеме, а давление – убыли внутренней энергии с увеличением обьема при постоянном значении энтропии.
Кроме того, изменение внутренней энергии системы при постоянном обьеме определяет величину теплового эффекта соотношением

Энтальпия.
По уравнению Н =f (р,S); энтальпия является характеристической функцией при независимых переменных р и S.
Следовательно: 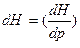 S
S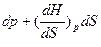 .
.
Изменение энтальпии системы при постоянном давлении определяет величину теплового эффекта соотношением


Из уравнения первого начало термодинамики 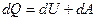 где
где  и
и  и при
и при  , получаем
, получаем 
А после интегрирования:
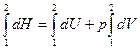

 .
.
Отсюда следует, что связь между функциями H и U определяется соотношением:
H=U+pV
Дифференцируя полученное выражение, получаем:
dH = d U+ pdV + Vdp
Далее подставляем значения dU из уравнения dU=TdS –pdV
dH = TdS –pdV + pdV +Vdp
после чего получаем
dH=TdS+VdP
Сравнивая уравнения 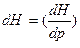 S
S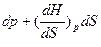 .и dH=TdS+VdP
.и dH=TdS+VdP
получаем, что
 ,
,
 .
.
Легко видеть, что температура является мерой возрастания энтальпии системы с увеличением энтропии при постоянном давлении, а обьем –мерой возрастания энтальпии системы с увеличением давления при постоянном значении энтропии.
Изохорно-изотермический потенциал.(Свободная энергия)
По уравнению F = f (V,T) свободная энергия является характеристической функцией при независимых переменных V и T.
Следовательно:

Согласно первомому началу термодинамики: 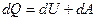 или dA = dQ –dU dA = TdS – dU
или dA = dQ –dU dA = TdS – dU

Если ввести обозначение
F = U-TS
то
A ,
,
т.е. работа системы при постоянной температуре и постоянном обьеме равна убыли функции Ғ в данном процессе. Из выражения F = U-TS следует, что при постоянной температуре и постоянном обьеме в работу не может перейти вся внутренняя энергия системы U. В работу превращается только ее часть, остающаяся вычета TS из U. Ее обозначили F и назвали свободной энергией.Таким образом,свободной энергией называется та часть внутренней энергии системы, которая можеть быть превращена в работу при постоянной температуре. Эта работа называется полезной и, если процесс протекает обратимо, является максимальной.
Та часть внутренней энергии, которая при постоянной температуре не превращается в работу TS, называется связанной или бесполезной энергией.
Чем больше энтропия системы, тем больше ее связанная энергия, поскольку энтропия представляет собой связанную энергию приходящуюся на 1 град.
Дифференцируя уравнения F = U-TS получаем:
df= dU- TdS-SdT
Далее подставляем, согласно уравнению
dU=TdS –pdV
поэтому
dF = -pdV –SdT
Сравнивая уравнения  и dF = -pdV –SdT, находим, что
и dF = -pdV –SdT, находим, что

и

Таким образом, давление является мерой убыли свободной энергии системы с увеличением обьема при постоянной температуре, а энтропия – мерой убыли свободной энергии с увеличением температуры при постоянном обьеме системы.
Изобарно-изотермический потенциал.
Термодинамический потенциал является характеристический функцией при независимых переменных р и Т, следовательно:

Так же как энтальпия отличается от внутренней энергии на величину рV,так и термодинамический потенциал отличается от свободной энергии на рV т.е.
dG= 
Проводя процесс при постоянном давлении и температуре, получаем

или, обозначая 
и принимая во внимания, что 
получаем 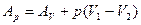
где Ар – полная максимальная работа системы, равная убыли термодинамического потенциала при постоянной при постоянном давлении. Она состоит из полезной максимальной работы системы А и работы сжатия р(V
и работы сжатия р(V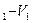 )
)
Дифференцируя уравнение dG=  g
g

dU = TdS –pdV
dG = Vdp-SdT



Легко видеть, что обьем системы является мерой возрастания термодинамического потенциала системы с увеличением давления при постоянной температуре, а энтропия –мерой убыли термодинамического потенциала с увеличением температуры при постоянном давлении.
Обьединенные первое и второе начало термодинамики (уравнение Гиббса - Гельмгольца)
Согласно уравнению F = U- TS и значению энтропии, которое дается выражением  , имеем
, имеем
F= U + T  .
.
Это и есть уравнение Гибсса-Гельмгольца для процессов, протекающих при постоянном обьеме. напишем это уравнение для двух состояний системы: 
и  .
.
Далее, вычитая одно из другого, получаем
 и
и 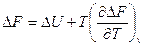
Отсюда: A
Согласно уравнениям  ,
,  и значению энтропии, которое дается уравнением
и значению энтропии, которое дается уравнением  ,имеем
,имеем
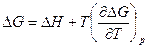 .
.
Это уравнение Гибсса –Гельмгольца для процессов, протекающих при постоянном давлении.
Направление протекания процессов и термодинамические условия равновесия.
Так как, согласно второму началу термодинамики, ив системе возможно только увеличение энтропии (при необратимых процессах), но не уменьшение и, как крайний случай, - сохранение постоянства энтропии (при обратимых процессах), то система находится в устойчивом равновесии, если ее энтропия максимальна в данных условиях.
Следовательно, общим условием протекания процессов в направлении устойчиого равновесия является условие
 ,
,
где знак равенства относится к равновесному состоянию, а знак неравенства к самопроизвольным процессам.
Условию равновесия можно придать и другие формулировки. Согласно уравнениям  и
и  , имеем
, имеем  и
и 
Таким образом, учитывая выражение  , при постоянной температуре и постоянном обьеме общим условием протекания процессов в направлении достижения устойчивого будет условие
, при постоянной температуре и постоянном обьеме общим условием протекания процессов в направлении достижения устойчивого будет условие
 ;
;
следовательно, при постоянной температуре и обьеме в любой системе самопроизвольно могут протекать только те процессы, которые сопровождаются уменьшением F, причем пределом их протекания, т.е. условием равновесия, является достижение некоторого минимального для данных условий значения F.
Точно так же при постоянной температуре и постоянном давлении общим протекания процессов и равновесия будет условие
dG  ;
;
следовательно, в системах, находящихся при постоянной температуре и постоянном давлении самопрозвольно могут протекать только процессы, сопровождаюшиеся уменьшением G, причем пределом их протекания, т.е. условием равновесия, служит некоторое минимальное значение G для данных условий.
Таким образом, при всех самопроизвольных процессах происходит уменьшение характеристических функций U,H,F и G, а равновесие характеризуется их минимальным для данных условий значением.
Химический потенциал.
В ходе химических процессов происходит не только изменение таких параметров ситемы, как обьем, давление и температура, но также изменяется состав. в приложении к таким системам для расмотрения равновесия Гиббс предложил использовать представление о химическом потенциале, который обозначается букой  с ссответствующими индексами.
с ссответствующими индексами.
Математически химические потенциалы представляют собой частные производные характеристических функций по числу молей данного компонента системы при постоянных значениях независимых параметров и количеств всех остальных компонентов.:

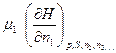 ;
;
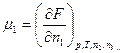 ;
;
можно ввести и через мольные концентрации (доли)х:
хі = n .
.
поскольку U,H, F и G являются функциями состояния, то при n = const имеем:
= const имеем:

и при хі =const имеем:
 ;
;
т.е. химический потенциал данного вешества і не зависит от выбора независимых переменных, определящих состояние системы.
Химический потенциал представляет собой фактор интенсивности химической э нергии данного вещества в системе, поскольку химическую энергию, подобно любомому другому виду энергии, можно рассматривать как произведение фактора интенсивности на фактор емкости. фактором емкости в данном случае будет число молей или концентрация данного вещества. Следовательно, приращение химической энергии можно представить в виде
нергии данного вещества в системе, поскольку химическую энергию, подобно любомому другому виду энергии, можно рассматривать как произведение фактора интенсивности на фактор емкости. фактором емкости в данном случае будет число молей или концентрация данного вещества. Следовательно, приращение химической энергии можно представить в виде 
 dx
dx .Кроме того, в состоянии равновесия не происходит превращений химической энергии, т.е.
.Кроме того, в состоянии равновесия не происходит превращений химической энергии, т.е.
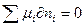
или 
Химический потенциал является мерой изменения характеристической функции при соответствующих постоянных параметрах и массах всех веществ, за исключением массы того компонента, количество которого изменяется в системе. Следовательно, химический потенциал можно рассматривать либо как соответствующий тепловой эффект (Q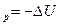 или Q
или Q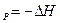 ), либо как совершаемую работу (A
), либо как совершаемую работу (A или А
или А )при изменении массы данного вещества в системе и заданном выборе переменных.
)при изменении массы данного вещества в системе и заданном выборе переменных.
Приближенные методы расчета теплоемкостей, теплот образования и сгорания химических соединении(метод А.Ф. Капустинского, метод тепловых поправок, методы расчета М.Х.Карапетьянца, уравнеие д.П.Коновалова и др.)Вычисление энтропии. Методика составления тепловых балансов химического процесса в изотермичесих и адиабатных условиях.
В основе термохимии лежит закон, согласно которому тепловой эффект реакции не зависит от промежуточных стадий и определяется лишь начальным и конечным состояниями системы. Этот закон был открыт путем сопоставления опытных данных, а затем экспериментально проверен Г.И. Гессом (1836-1840 гг.)
Закон Гесса имеет большое практическое значение. Например, с его помощью можно установить тепловые эффекты реакций, экспериментальное определение которых представляет большие трудности.
Для этих целей широко используются следствия из закона Гесса:
Первое следствие: тепловой эффект разложения какого-либо химического соединения равен по абсолютной величине и противоположен по знаку тепловому эффекту образования этого соединения.
Второе следствие: если совершаются две реакции, приводящие из различных начальных состояний к одинаковым конечным, то разница между тепловыми эффектами представляет собой тепловой эффект перехода из одного начального состояния в другое.
Третье следствие: если совершаются две реакции, приводящие из одинаковых начальных состояний к различным конечным, то разница между их тепловыми эффектами представляет собой тепловой эффект перехода из одного конечного состояния другое.
Например, двуокись углерода можно получит, сжигая углеродв кислороде непосредственно до двуокиси углерода
С+О2= СО2 +Q1, Q1= 94,05 ккал или получая окись углерода, а затем сжигая ее до двуокиси:
C+1/2O2= CO+ Q2, Q1= 26,4 ккал
CO+1/2 O2 = CO2 +Q3 Q2= 67,63 ккал
Оба эти пути имеют одинаковое начальное состояние (C иO2) и одинаковое конечное состояние (СО2). Под одинаковостью состояния подразумевается полное тождество по химическому составу, по условиям существования(температура, давление и др.), по агрегатному состоянию и кристаллической модификации, по степени дисперсности и т.п.
По закону Гесса, тепловой эффект сжигания углерода должен быть равен суммарному тепловому эффекту при сжиганим его через окись углерода, т.е.
Q1=Q2 +Q
Тепловой эффект и теплота реакции.
При протекании химических реакций происходит глубокое изменение вещества, сопровождающееся или поглощением или выделением теплоты. Знание тепловых эффектов, сопровождающих реакции, позволяет сознательно управлять им, меняя соответствующим образом внешние условия среды.
Многобразие химических превращений по тепловомому балансу можно разделить на две группы: реакции, протекающие с выделением теплоты, - экзотермические и реакции, протекающие с поглощением теплоты, - эндотермические.
К экзотермическим реакциям относится большинство реакций с образования химических соединений из простых веществ:
С+О2 = СО2 + 94,05 ккал
К эндотермическим реакциям относится больщинство реакций диссоциации химических соединений на простые вещества, например:
2Н2О =2Н2 +О2 -136,64 ккал
Существует реакции, сопровождающие выделением или поглощением незначительного количества тепла, а при некоторых условиях тепловой эффект может стать нулевым, например
КІ +І2 = КІ3 +0,8 ккал.
На общее выделение или поглощение теплоты при той или иной химической реакции заметное влияние оказывают такие физическое явления, как переход реагирущих веществ из одного состояния в другое, поскольку все подобные переходы связаны с поглощением или выделением энергии:
Н2О (тв.) = H2O (жидк.) -1,44 ккал,
C(алмаз)= C(графит) + 0,45 ккал.
Поэтому термохимические уравнения должны содержать указание на агрегатное состояние продуктов реакции, а для кристаллических веществ – указание на их модификацию, если возможно их существование в нескольких модификациях.
Когда из простых вешеств образуется какое-либо соединение, то этот процесс сопровождается некоторым тепловым эффектом. Количество теплоты при этом не одинаково для различных соединений; кроме того, значения тепловых эффектов существенно меняются с изменением внешних параметров системы.
Теплотой образования принято называть тепловой эффект реакции образования 1 моль данного соединения из простых вешеств.
Стандартной теплотой образования называют теплоту образования соединения, отнесенную к температуре 25оС (298оК) и 1 ат(760 мм.рт.ст.)
Если известна эта величина, то термохимический расчет позволяет определить теплоту образования при других значениях параметров состояния.
Практическое значения теплот образования заключается в том, что, зная теплоты образования всех веществ, участвующих в той или иной реакции, можно рассчитать тепловой эффекет этой реакции. Так, согласно закону Гесса, тепловой эффект реакции равен разности между суммой теплот образования конечных продуктов и суммой теплот образования исходных веществ с учетом коэффициентов при формулах этих веществ в уравнении реакции.

При этом необходимо помнить, что для тех реакций, в которых участвуют простые вещества, теплота образования этих простых веществ условно принято равной нулю.
Например, если известно,что
1) S + O2 = SO2 + 70,94 ккал;
2) 2Cu +S = Cu2S +19,0 ккал;
3) 2Cu +1/2 O2 = Cu2O +39,89 ккал,
то имеется возможность определить тепловой эффект реакции:
2Cu2O +Cu2S =6Cu +SО2+Q
Подсчет по теплотам образования дает:
1 ккал
ккал
Полученный результат легко проверить.Для этого необходимо из первого уравнения вычесть второе и удвоенное третье уравнение.
Теплотой сгорания называется тепловой эффект реакции полного сгорания одного моля данного соединения до образования высших окислов.
Поскольку с изменением температуры и давления величина теплоты сгорания может существенно меняться, то для термохимических расчетов важно ввести представление о стандартной теплоте сгорания.
Стандартной теплотой сгорания называется теплота сгорания, отнесенная к стандартным условиям, т.е. 25оС (298оК) и 1 ат(760 мм.рт.ст.)
Практическое значение теплот сгорания состоит в том, что по ним непосредственно можно определять тепловые эффекты реакций, так как тепловой эффект реакции равен разности между суммой теплот сгорания исходных веществ и суммой теплот сгорания конечных продуктов с учетом коэффициентов при формулах этих веществ в уравнении реакции.

например, необходимо определить теплоту образования метана из элементов по реакции С +2Н2= СН4 +Q если известно, что
1) C+ O2 = CO2 +94,05 ккал
2) H2 +1/2 O2 =H2O +68,32 ккал
3) CH4 +2O2 = CO2 +2H2O +211,93 ккал
Производим подсчет:
Q = 1 ккал
ккал
Зависимость теплового эффекта от температуры (закон Кирхгофа)
Очень часто бывает необходимо знать тепловые эффекты реакций при высоких температурах, в то время как таблицы термохимических величин содержат только стандартные тепловые эффекты, относящиеся к температуре 25оС(298оК). Первое начало термодинамики позволяет определить зависимость тепловых эффектов от температуры и производить соответствующие пересчеты.
Зависимость теплового эффекта реакции от температуры (при постоянных давлении или обьема)пределяется уравнениями Кирхгофа:
(d Qv/dT)v = (d U /dT)v =
U /dT)v =  Cv (1)
Cv (1)
(dQp /dT)p = (d H /dT)p =
H /dT)p =  Cp (2)
Cp (2)
где  C =
C =  (nC)прод. –
(nC)прод. –  (nC)исх. Разность сумм молярных теплоемкостей Ср или С продуктов реакции и исходных веществ, взятых с учетом стехиометрических коэффициентов.Уравнение Кирхгофа в интегральной форме имеет вид:
(nC)исх. Разность сумм молярных теплоемкостей Ср или С продуктов реакции и исходных веществ, взятых с учетом стехиометрических коэффициентов.Уравнение Кирхгофа в интегральной форме имеет вид:
 H2 =
H2 =  H1 +
H1 +
 CpdT
CpdT
Зависимость теплоемкости от температуры Cp = f(T) выражается в виде одного из двух эмпирических степенных рядов:Cp = a+bT +cT-2(3) или
Cp = a+bT +cT2 (4)
Отсюда
 Cp =
Cp =  a +bT +
a +bT +  cT2 +
cT2 +  cT-2 (5)
cT-2 (5)
после подстановки уравнения в уравнение и интегривования получим зависимость теплового эффекта от температуры:
 H =
H =  Ho +
Ho + aT + ½
aT + ½  bT2 +1/3
bT2 +1/3  cT3 -
cT3 - cT-2 (6)
cT-2 (6)
Где  Ho- постоянная интегрирования, которая определяется по полученному опытному тепловому эффекту при одной какой-либо температуре.
Ho- постоянная интегрирования, которая определяется по полученному опытному тепловому эффекту при одной какой-либо температуре.
Интегрирование уравнения (2) после подстановки (5) можно вестив интервале температур от Т1 и Т2.При этом получим
 H2 =
H2 =  H1 +
H1 +  a (T2-T1)+1/2
a (T2-T1)+1/2  b(T22 –T12)+
b(T22 –T12)+ 1/3 (T23 –T13)+
1/3 (T23 –T13)+  c(1/T1 -1/T2)
c(1/T1 -1/T2)
1) Для неорганических веществ в приближенном состоянии применяется метод Капустинского.

 - валентность
- валентность
z-порядковый номер
а,в – эмперические постоянные.
2)Расчет теплоты образования вешества по энергиям химических связей.
В этом расчете сначала предполагают разложение исходных простых веществ на атомы, а затем образование из них конечного газообразного соединения. Первый этап связан с затратой энергии на разрыв связей в исходных простых веществах, а второй- с выделением энергии образования новых связей. Поэтому теплоты образования газообразного вещества в соответствии с законом Гесса можеть быть определена по уравнению
 ,
,
где n –  число связей данного вида;
число связей данного вида;  -энергия разрыва или образования связи; n*- число атомов твердых элементов;Q
-энергия разрыва или образования связи; n*- число атомов твердых элементов;Q -теплота возгонки твердого элемента.
-теплота возгонки твердого элемента.
Энергия химической связи –это доля поглощенной энергии, которая приходится на данную связь при полной диссоциации молекулы на свободные атомы.
3)Для большинство химических веществ теплота сгорания могуть быть определены по формуле Коновалова.

m –число атомов О2, необходимых для полного сгорания данного соединения.
n- число молей образующейся воды
х- поправка, постоянная в пределах данного гомологического ряда.
Первое начало термодинамики.
Первое начало термодинамики представляет собой частный случай закона сохранение материи и расматривает сохранение энергии при различных превращениях одних форм движение материи в другие.
Представим себе,что перевод вещества из состояния 1 в состояние 2 связан с изменением внутренней энергии  , а при обратном переходе из состояния 2 в состояние 1 другим путем изменение внутренней энергии составляет
, а при обратном переходе из состояния 2 в состояние 1 другим путем изменение внутренней энергии составляет  . Таким образом изменение внутренней энергии системы при любом процессе зависит не от пути этого процесса, а лишь от начального и конечного состояний. Изменение внутренней энергии будем считать положительным, если процесс сопровождается приращением внутренней энергии системы. Отрицательное значение будеть соответствовать убыли внутренней энергии.
. Таким образом изменение внутренней энергии системы при любом процессе зависит не от пути этого процесса, а лишь от начального и конечного состояний. Изменение внутренней энергии будем считать положительным, если процесс сопровождается приращением внутренней энергии системы. Отрицательное значение будеть соответствовать убыли внутренней энергии.
Теперь первое начало термодинамики можно представить в виде уравнения
dQ = dU +dA
Уравнение соответствует следующему положению: поглощаемое системой тепло расходуется и наувеличение внутренней энергии системы и на совершение внешней работы – работы расширения.
Второе начало термодинамики.
Подобно тому, как первое начало вводит функцию состояния – внутреннюю энергию, второе начало в форме, приданной ему дальнейшими работами Клаузиуса, вводит функцию состояния, названную энтропией.
Согласно второму началу, в то ремя как внутренняя энергия изолированной системы остается неизменной, ее энтропия при всех самопроизвольных процессах увеличивается.
Энтропия (S) – термодинамическая функция состояния, которая служит мерой беспорядка (неупорядочности) системы. Возможность протекания эндотермических процессов обусловлена изменением энтропии, ибо в изолированных системах самопроизвольно протекающего процесса увеличивается  S
S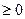 (второй закон термодинамики). S=R*lnW
(второй закон термодинамики). S=R*lnW
Размерность энтропии 1 моля вещества совпадает с размерностью газовой постоянной R и равна Дж*моль -1 S
 S
S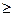 Q/T и
Q/T и S=Q/T
S=Q/T
Для химической реакции изменение энтропии аналогично энтальпии термин был введен Клаузиусом (1985 г.) через отношение Q/T (приведенное тепло).
dS = dQ/T
где dS –дифференциал энтропии; dQ-дифференциал теплоты; Т- абсолютная температура;
Это формула является математическим выражением классической формулировки 2 закона термодинамики, который гласит, что для всех обратимых изменений в закрытой системе с однородной температурой справедливо соотношение
dS = dQ/T
Для всех необратимых изменений в закрытой системе величина приращения энтропии будет больше, чем изменение приведенной теплоты, то есть
dS 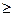 dQ/T
dQ/T
При чем знак равенства имеет место при обратимых процессов, а неравенства – при необратимых процессах.
Запишем формулировку второго закона термодинамики:
У всякой изолированной системы, находящейся в неравновнсном состоянии, энтропия с течением времени возрастает, ее рост продолжается до тех пор,пока система не достигнет равновесного состояния.
Вычисление энтропии.
При переходе из состояния 1 в состояние 2 изменение энтропии определяется соотношением
dS =dQ/T
Изменение энтропии в сложном процессе равно сумме изменений энтропии в отдельных стадиях процесса.Абсолютное значение энтропии какого-либо вещества при любой температуре можно расчитать, если известна абсолютная величина энтропии S1 при какой –либо одной температуре:
S2= S1 + S
S
Значение S1 находят из справочных таблиц при 25оС и стандартном давлении 1 атм.
Изменение энтропии вычисляют по следующим уравнениям:
1. Изменение энтропии при нагревании n молей любого вещества от температуры Т1 до Т2 при Р= const рассчитывается по формуле
 S = S2-S1 = n
S = S2-S1 = n 

Если зависимость Ср от температуры описывается выражением
Cp = a+bT +cT2
то  S = 2303na lg
S = 2303na lg 
 + nb (T2-T1)+ n
+ nb (T2-T1)+ n (T22 –T12)
(T22 –T12)
2.Изменение энтропии при фазовом переходе рассчитывается по формуле
 S=
S= 
 H /T
H /T
где Н – теплота фазового перехода одного моля вещества;
Н – теплота фазового перехода одного моля вещества;
Т – абсолютная температура фазового перехода.
3. Изменение энтропии при переходе
н молей идеального газа из одного состояния в другое вычисляется по уравнениям:
 S=2303 nCvlg
S=2303 nCvlg

или  S =2303nalg
S =2303nalg 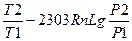
или  S =2303 nCvlg
S =2303 nCvlg
где V1,P1,T1 и V2,P2,T2 -обьем, давление, температура, характеризующие начальное и конечное состояние идеального газа соответственно; Cp и Cv- соответственно истинные теплоемкости идеального газа при постоянных давлении и обьеме;
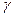 =Cp/Cv
=Cp/Cv
4. Изменение энтропии в процессе диффузии при смешении идеальных газов (при Р=const и T= const) т.е. в изотермно-изобарном процессе, вычисляются по уравнению
 S= 2303R (n1lg V1/V2
S= 2303R (n1lg V1/V2  +n2 lg V1/V2)
+n2 lg V1/V2)
или S= -2303R(n1+n2)[N1lgN1 +N2lgN2]
S= -2303R(n1+n2)[N1lgN1 +N2lgN2]
где n1,n2 – число молей первого и второго газа;N1,N2 – мольные доли обоих газов;V1,V2 – начальные обьемы обоих газов;V – конечный обьем смеси газов V=V1+V2.
5. Вычисление изменения энтропии по электрохимичческим данным по уравнению
 S=
S=  H +
H + zFE/T
zFE/T
где  Н –тепловой эффект химической реакции; F-число Фарадея;Е –электродвижущая сила э.д.с. электрохимического элемента, вкотором протекает данная реакция; z –число электронов
Н –тепловой эффект химической реакции; F-число Фарадея;Е –электродвижущая сила э.д.с. электрохимического элемента, вкотором протекает данная реакция; z –число электронов
Химическая система находится в равновесии,если ее состояние при заданных состояние при заданных состояние внешних условиях (например, температуре и давлении) во времени не изменяется.
Кроме того,равновесие не означает полного покоя. Напротив, при равновесии в системе идут процессы, но в противоположных направлениях, так что их результаты взаимно уничтожаются.
рассмотрим химическую реакцию в гомогенной газовой среде:
bB +dD  gG +rR,
gG +rR,
где b,d,g и r представляют собой стехиометрические коэффициенты соответствующих веществ B,D,G и R.Между веществами B и D существет сродство, т.е. стремление к взаимодейстию. Оно же имеется и у веществ G и R. Следовательно, реакция протекает в обоих противоположных направлениях. Для скоростей обеих противоположных направленных реакций (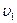 и
и  )можно составить следующие выражения:
)можно составить следующие выражения:

и

где k и k
и k -константы скоростей реакций, а C
-константы скоростей реакций, а C - молярные концентрации, которые, будучи возведенными в соответсствующие степени определяют скорости реакций
- молярные концентрации, которые, будучи возведенными в соответсствующие степени определяют скорости реакций 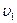 и
и  .
.
Если  , то молекул G и R будет образовываться больше, чем молекул B и D (при этом концентрации C
, то молекул G и R будет образовываться больше, чем молекул B и D (при этом концентрации C и С
и С уменьшаются, а концентрации С
уменьшаются, а концентрации С и С
и С увеличиваются). Если
увеличиваются). Если  , то больше будет образовываться молекул В и D, а не G и R(C
, то больше будет образовываться молекул В и D, а не G и R(C и C
и C увеличиваются,а С
увеличиваются,а С и С
и С уменьшаются).Наконец,если
уменьшаются).Наконец,если  , т.е. обе реакции протекают с одинаковыми скоростями, то никаких видимых изменений происходить не будет, так как в единицу времени будет образовываться одинаковое число молекул B, D,G и R. При этом устанавливается равновесие и, пользуясь выражениеями для скоростей прямой и обратной реакций, можно подойти к весьма важному понятию о константе равновесия:
, т.е. обе реакции протекают с одинаковыми скоростями, то никаких видимых изменений происходить не будет, так как в единицу времени будет образовываться одинаковое число молекул B, D,G и R. При этом устанавливается равновесие и, пользуясь выражениеями для скоростей прямой и обратной реакций, можно подойти к весьма важному понятию о константе равновесия:


откуда К =  ,
,
где К- константа равновесия, равная отношению констант скоростей прямой и обратной реакций. Следовательно, для составления выражения константы равновесия в числителе дроби пишется произведение концентраций веществ левой части уравнения, в знаменателе –праой части уравнения.
Константа равновесия связывает концентрации всех веществ, участвующих в реакции, и нельзя изменить концентрацию ни одного из них, чтобы это не повлекло за собой соответствующего изменения концентраций всех остальных веществ, участвующих в реакции, которое приводит к прежнему численному значению константы равновесия при данных условиях. Таково содержание закона действия масс.
Константы равновесия химической реакции, протекающей в смеси идеальных газов по уравнению
аА + bВ = Gg +Rr
где a,b,g,r – стехиометрические коэффициенты участвующих в реакции веществ A,B,G,R имеет следующий вид:
Kp =

Где Кр – константа химического равновесия; р- равнове
– константа химического равновесия; р- равнове сные парциальные давления.
сные парциальные давления.
Константа равновесия Кр не зависит от давления. Учитывая соотношения между парциальным давлением, концентрацией и мольной долей газа і-го сорта
Можно получить также выражения для константы равновесия химической реакции:
Kс = ; КN=
; КN= ;
;
Где Р –общее давление;ni – число молей і-го компонента;  -общее число молей реагентов в равновесной газовой смеси.
-общее число молей реагентов в равновесной газовой смеси.
Константы равновесия Кр,Кс,КN связаны соотношением
Кр = Кс(RT) = КNP
= КNP
 = g+r –a-b –разность между стехиометрическими коэффициентами конечных и начальных газообразных веществ в соответствии с уравнением реакции. Константа равновесия КN
= g+r –a-b –разность между стехиометрическими коэффициентами конечных и начальных газообразных веществ в соответствии с уравнением реакции. Константа равновесия КN
 зависит от общего давления. Если
зависит от общего давления. Если  =0, то Кр = Кс =КN
=0, то Кр = Кс =КN
Это означает, что при  =0 численные значения
=0 численные значения  константы равновесия при любом способе выражения концентрации одинаковы.
константы равновесия при любом способе выражения концентрации одинаковы.
Для гетерогенных реакций с участием газообразных веществ константы равновесия Кр выражается только отношением равновесных парциальных давлений газообразных реагентов. Давление насыщенных паров твердых илижидких веществ, участвующих в реакции, не зависит от количества конденсированной фазы и при постоянной температуре остается постоянным. Например, для реакции аА(т)+ bB(г)  gG(г)
gG(г)
Kp = 
Константу рановесия химической реакции можно вычислить пользуясь стандартными изменениями изобарных потенциалов.

Определение направление процесса по уравнению изотермы химической реакции.
Изменение изобарного потенциала при протекании химической реакции в газовой фазе
аА + bВ = Gg +Rr
при постоянном давлении и постоянной температуре можно вычислить по уравнению изотермы

pG, pR,pA,pB – любые взятые в реакцию парциальные давления реагирующих веществ.
Уравнение изотермы можеть быть записано также следующим образом ()

CG,CR,CА,CB-любые взятые концентрации реагирующих веществ.
По знаку 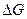 и
и 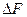 можно судить о возможности протекания данной реакции. Если согласно расчету (
можно судить о возможности протекания данной реакции. Если согласно расчету (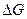 )p,T
)p,T  , то реакция может протекать самопроизвольно в прямом направлении.(
, то реакция может протекать самопроизвольно в прямом направлении.(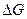 )p,T
)p,T , то данная реакция в прямом направлении самопроизвольно протекать не может. При (
, то данная реакция в прямом направлении самопроизвольно протекать не может. При (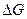 )p,T=0,система находится в равновесии.
)p,T=0,система находится в равновесии.
Приближенные данные о протекании реакции можно также получить по стандартному изменению изобарного потенциала реакции, которое определяется по уравнению
 реакц=
реакц= 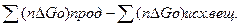
Если согласно расчету 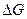 о реакц
о реакц  ,то реакция будет протекать;если
,то реакция будет протекать;если 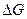 о реакц
о реакц  , то реакция не пойдет.
, то реакция не пойдет.
Расчеты по уравнениям изобары и изохоры химической реакции.
Зависимость константы равновесия от температуры.
Влияние температуры на константу равновесия выражается уравнениями изобары и изохоры:
 или
или  при р = const и называется уравнениями изобары химической реакции. Полученные уравнения устанавливают связь между изменениями константы равновесия с температурой и тепловым эффектом реакции.
при р = const и называется уравнениями изобары химической реакции. Полученные уравнения устанавливают связь между изменениями константы равновесия с температурой и тепловым эффектом реакции.
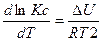 или
или  при V = const и называются уравнениями изохоры химической реакции.
при V = const и называются уравнениями изохоры химической реакции.
Если допустить в первом приближении, что  , то тогда в интегральной форме уравнение имеет следующий вид:
, то тогда в интегральной форме уравнение имеет следующий вид:
Lg Kp= -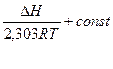
Интегрирование в пределах от Т1 до Т2 дает
lg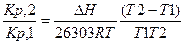
Расчеты по равновесиям с помощью таблиц стандартных величин.
Существуют три вида таблиц стандартных величин:1) таблицы изменений энтальпии при образовании одного моля при стандартных условиях; 2) таблицы изменений изобарного потенциала образования одного моля вещества при стандартных услоиях;3)таблицы энтропий, рассчитанных на 1 моль вещества при стандартных условиях.
Таблицы стандартных величин позволяет определить  реакции только при стандартных условиях. Для нахождения этих величин при любой температуре нужно знать математическую эависимость их от температуры.
реакции только при стандартных условиях. Для нахождения этих величин при любой температуре нужно знать математическую эависимость их от температуры.
Согласно уравнению Кирхгофа  Cp =
Cp =  a +bT +
a +bT +  cT2 +
cT2 +  cT-2
cT-2
имеем: 
или 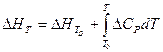
где 
Если  , то
, то

Согласно уравнению  имеем:
имеем:
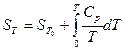
или, если Т , то
, то


Если уравнение  или
или
 подставить в уравнение
подставить в уравнение  то получим:
то получим:

Теплоемкости, которые помещены под знаком интеграла, также зависит от температуры.
При любой температуре Т

Для практических целей удобней пользоваться уравнением, в котором натуральный логарифм переведен в десятичный, а универсальная постоянная выражена в калориях. Тогда

таким образом, получив значения 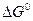 по уравнению легко находим значение константы равновесия при данной температуре.
по уравнению легко находим значение константы равновесия при данной температуре.
 .
.
Термодинамика газожидкофазных превращений. Реальные газы.Уравнения состояния реальных газов и смесей.Классификация методов получения низких температур.
При расчете бинарного равновесия газ-жидкость рассматривают изотермический и изобарический варианты представления зависимостей давления паров и температур кипения от состава фаз:
Р= 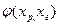
 Для каждого компонента паровой и жидкой смеси условие термодинамического равновесия дается в виде равенства фугитивностей паровой и жидкой фаз: fі, г =
Для каждого компонента паровой и жидкой смеси условие термодинамического равновесия дается в виде равенства фугитивностей паровой и жидкой фаз: fі, г =  p.
p.
Коэффициент фугитивности компонента паровой смеси  рассчитывают с учетом влияния давления Р, обьема V и температуры T, а также содержания других компонентов в фазе. Фугитивность компонента жидкой смеси
рассчитывают с учетом влияния давления Р, обьема V и температуры T, а также содержания других компонентов в фазе. Фугитивность компонента жидкой смеси  зависит от коэффициента активности
зависит от коэффициента активности  , молярной доли
, молярной доли 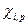 и стаандартной фугитивности чистого компонента
и стаандартной фугитивности чистого компонента  при температуре Е и общем давлении системы Р:
при температуре Е и общем давлении системы Р:

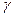
Уравнение представляяет собой математическое отображение обьединенного закона Рауля –Генри для летучих растворителя и растворенного вещесва.
Коэффициент активности  компонента раствора играет важную роль в расчетах равновесия пар-жидкость. По уравнениям
компонента раствора играет важную роль в расчетах равновесия пар-жидкость. По уравнениям  и
и  коэффициенты активности индивидуальных компонентов раствора связаны между собой, в том числе и для бинарной смеси, зависимостью:
коэффициенты активности индивидуальных компонентов раствора связаны между собой, в том числе и для бинарной смеси, зависимостью:

Последнее уравнение интегрируют и используют для нахождения коэффициента активности  в зависимости от
в зависимости от  , если имеются экспериментальные зависимости
, если имеются экспериментальные зависимости  . В том случае, когда получены данные о
. В том случае, когда получены данные о  и
и  при определенных значениях
при определенных значениях  и
и 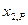 , можно их проверить на термодинамическую совместимость, используя закон Гиббса –Дюгема.
, можно их проверить на термодинамическую совместимость, используя закон Гиббса –Дюгема.
Уравнения Гиббса –Дюгема –Маргулиса:

ni – число молей каждого компонента вне зависимости от ида присутствующих в растворе соединений. Оно вытекает из анализа общего значения изменения энепгии Гиббса  многокомпонентного раствора
многокомпонентного раствора

При постоянных Р и Т уравнение превращается в уравнение 
Из равенства  следует, что при данном составе в состоянии равновесия любые изменения химических потенциалов одних компонентов раствора сопровождаются противоположным изменением потенциалов других компонентов.
следует, что при данном составе в состоянии равновесия любые изменения химических потенциалов одних компонентов раствора сопровождаются противоположным изменением потенциалов других компонентов.
Активность летучих компонентов раствора
а
Активность растворенных неорганических веществ обобщается равенством:

Многие практические задачи в системах раствор –пар решают с помощью законов Гиббса –Коновалова. Эти законы устанавливают существенные качественные взаимосвязи температуры, давления и составов жидкой и паровой фаз.
Согласно первомому закону пар относительно богаче тем компонентом, прибавление которого к смеси вызывает повышение давления пара при заданной температуре или понижение температуры кипения раствора при неизменном давлении.
 если
если 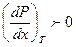
вторая часть –неравенству:  если
если 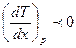
Второй закон гласит: с увеличением концентрации любого компонента бинарной смеси в жидкой фазе возрастает его концентрация в паровой фазе.Следовательно

Третий закон для постояннокипящих смесей устанавливает: в точках экстремума кривых, выражающих зависимость температуры кипения(p=const) или давления(T=const) паров смесей от состава, жидкость и пар имеют одинаковый состав. Согласно этому закону, при образовании азеотропа  , а также
, а также
 и
и 
Классификация методов получения низких температур.
Применение охлаждения метода технологической обработки в химической промышленности, металлургии, электротехники, атомной технике, энергетике, а также в медицине, быту и прочих областях непрерывно расщиряется. Увеличивается число процессов, где этот метод дает существенный эффект. Совершенствование техники низких температур привело к снижению себестоимости холода. Оба эти обстоятельства позволяют ожидать дальнейшего расширения использования метода охлаждения химических систнм как одного из методов химико-технологической обработки.
Условно криологию можно разделить на два крупных раздела- техника умеренного охлаждения и техника глубокого охлаждения, которые имеют теоретические позиции, но существенно различаются по основным методам создания холодильных эффектов и их применения.
Область умеренного охлаждения ограничивают ттемпературным интервалом от 2830С до  120 К.К области глубокого охлаждения относят температуры ниже 120К. вплоть до температуры, близкой к абсолютному нулю. Методы криогенной техники используют при производстве ожиженных газов. Благодаря ее методам изучены свойства сверхпроводимости и сверхпроводимости и сверхтекучести, проявляющиеся при очень низких температурах.
120 К.К области глубокого охлаждения относят температуры ниже 120К. вплоть до температуры, близкой к абсолютному нулю. Методы криогенной техники используют при производстве ожиженных газов. Благодаря ее методам изучены свойства сверхпроводимости и сверхпроводимости и сверхтекучести, проявляющиеся при очень низких температурах.
Получение холода в промышленных условиях основано на том, что при помощи холодильного агента от технологического обьекта охлаждения отбирается теплота и передается окружающей среде.
Холодильные агенты, или рабочие тела холодильных устройств –это вещества, в результате физико-химических или физичческих превращений которых создаются условия для охлаждения технологического обьекта.
К понижению температуры холодильногоагента приводят следующие группы процессов:
Фазовые превращения – испарение, плавление, возгонка, растворение- холодильного агента с передачей ему от охлаждаемого обьекта теплоты, эквивалентной теплоте фазового превращения.
Адиабатическое изоэнтропийное расширение сжатого газа при совершении внешней работы или изоэнтальпийное дросселирование сжатого газа или жидкости без получения внешней работы;оба вида охлаждения достигаются за счет внутренней энергии рабочего тела;
Физические превращения твердых рабочих тел с проведением десорбции, адиабатного размагничивания, адиабатного сжатия, термоэлектрического и термомагнитного воздействий.
Химическая кинетика –
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 389; Нарушение авторских прав?; Мы поможем в написании вашей работы!