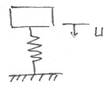
Свободные колебания системы с одной степенью свободы

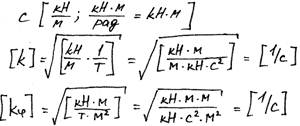
Будем исходить из уравнения (19)

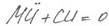(1/м);

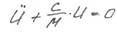- дифференциальное уравнение II порядка с постоянными коэффициентами.

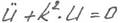, где

Пусть

(б) à в (а), получим:

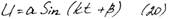
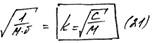- частота колебаний [1/c]

Бывает двух типов:

- циклическая;

- техническая.

Циклическая частота – количество колебаний за 2p сек.

Техническая частота – количество колебаний за 1 сек.

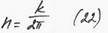, [Гц]

Период колебаний – продолжительность одного полного колебания.

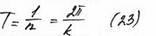,[c]

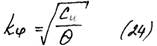
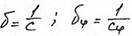
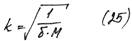
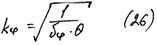
b-начальная фаза (из (20))

а – амплитуда- максимальное отклонение от положения статического равновесия.

Значения а и b определяются по начальным условиям.

Т.к. здесь два параметра, то и условий два:

1) при t=0, U=U0 – начальное перемещение;

2) при t=0, (U’=U0’) - начальная скорость.

Подставим первое условие в (20):

1)

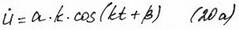
Подставим второе условие в (20 а):

2)

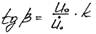
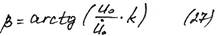
Возведем в квадрат оба (*) и сложим их:

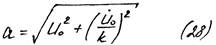
Видим, что амплитуда зависит от начальной скорости и начального перемещения.

При отсутствии сопротивления в системе, колебания носят незатухающий гармонический характер с частотой, которая является собственной для системы.

Изменение собственной частоты возможно, но за счет:

1. изменения инертности (массу, либо момент инерции);

2. изменение жесткости упругой связи.

Дифференциальное уравнение систем с одной степенью свободы в обратной форме.

Вывод уравнений движения выполнен на основе правила Даламбера и независимости действия сил.

Кроме фактических действующих сил необходимо учесть силы инерции на ускорение.

F – равнодействующая всех сил, действующих на систему (в том числе и силы упругости).

Учтем следующие силы:

1) Внешние:

Fвн. = F (t) – направим в направлении положительного перемещения системы.

2) Силы инерции:

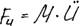– направим в противоположную сторону Fвн (или перемещения).

Дата добавления: 2014-01-06