Силы неупругого сопротивления (трения)

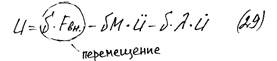– вынужденные колебания системы с сопротивлением.

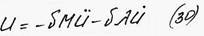– свободные колебания системы с сопротивлением (частный случай).

– свободные колебания системы без сопротивления.

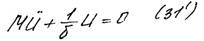
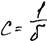(5)

Свободные затухающие колебания системы с одной степенью свободы при наличии вязкого трения.

Будем использовать для описания колебаний дифференциальное уравнение в прямой форме.

(18)

Обозначим 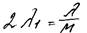(а), разделим на массу.

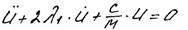- дифференциальное уравнение II порядка с постоянным коэффициентом. (21)

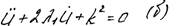
Рассмотрим два возможных варианта решения:

1.Случай большого сопротивления (l > k)

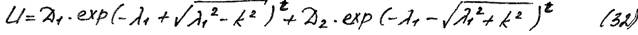
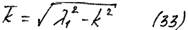
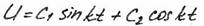
2. Случай малого сопротивления (l < k).

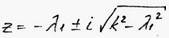корни будут комплексны

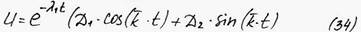
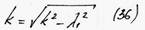- частота системы с трением

Пусть 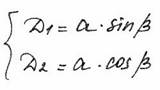перейдем к одночленной форме записи, заменяя D1 и D2 на a и b.

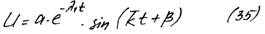
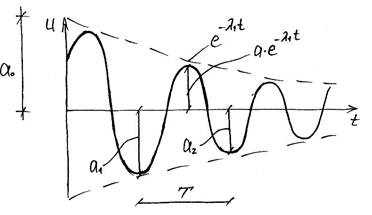
Колебание такой системы представляет собой затухающую синусоиду, у которой амплитуда уменьшается со временем, а частота колебаний отличается от частоты колебаний системы с трением.

Оценим влияние трения на частоту и амплитуду.

Для конструкций, у которых развивающееся максимальное трение l1 оценивается в ней

l1 = 0,1 k (*)

Подставим (*) в (36)

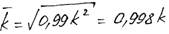
Влияние трения на частоту свободных колебаний оценивается величиной не больше 0,2 %, поэтому в расчетах собственных частот в строительных конструкциях влиянием трения можно пренебречь.

Оценим влияние трения на амплитуду колебаний.

Для описания степени затухания введем величину, равную ln отношению соседних амплитуд.

l1 = 0,1 k;

При сильном колебании амплитуда уменьшается почти в 2 раза за 1 период.

Для различных материалов логарифмический декремент (d) составляет:

- для бетона 0,3 – 0,4

- для стали 0,1 – 0,15

- для дерева 0,15 – 0,2

Амплитуда и начальная фаза в случае затухающих колебаний определяется из начальных условий.

1) при t=0, U=U0

2) при t=0, U’=U0’

Подставим первое условие в (34)

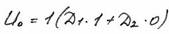
D1= U0

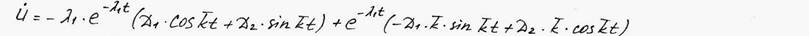
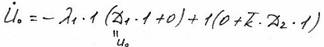
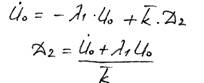
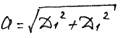
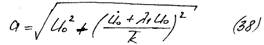
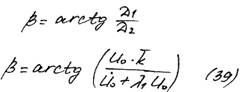
Сопоставляя (38) и (39) с формулами (27) и (28), замечаем, что сопротивление оказывает влияние и на амплитуду, и на начальную фазу.

Вынужденные колебания системы с одной степенью свободы при наличии силового гармонического возмущения.

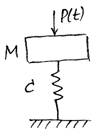Рассмотрим колебания на основе уравнения в прямой форме, при этом в первом приближении не будем учитывать затухающие колебания. В качестве возмущения будем использовать гармоническую функцию.

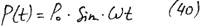
Р0 – амплитудное значение возмущающей силы.

Такое силовое возмущение является широко распространенным, например, воздействие на строительную конструкцию при работе станка с эксцентрично расположенной вращающейся частью.

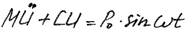(17) (без λ*U')

Это дифференциальное уравнение II порядка неоднородное, его решение можно записывать в следующем виде: Uон = Uоо + Uчн

Uоо – решение уравнения MÜ + сU = 0

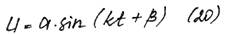
Найдем Uчн:

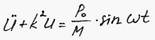
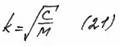– собственная частота.

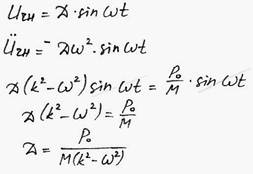
Дата добавления: 2014-01-06