Теорема Остроградского-Гаусса

Поток вектора напряженности.

Лекция 2

По определению потоком векторного поля 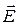через площадку 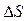, рис.2.1, называется величина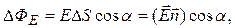

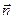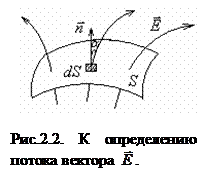
где - вектор нормали к площадке 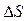. Если поле неоднородно или поверхность, через которую вычисляется поток, не является плоской, рис.2.2, то определение потока нужно применить к бесконечно малому элементу поверхности, а именно записать:

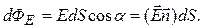
Тогда поток через всю поверхность S будет:

,

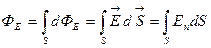где 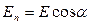- проекция вектора 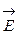на направление вектора .

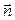Таким образом, поток – величина алгебраическая. Знак потока зависит от выбора направления нормали к элементарным площадкам, на которые разбивается поверхность S при вычислении Ф_Е. Изменение направления нормали на противоположное изменит знак E_n, а значит и знак потока Ф_Е. В случае замкнутых поверхностей принято считать знак потока положительным, если силовые линии поля выходят из охватываемой области наружу. Если густоту силовых линий (т.е. их число, пересекающих единичную площадку) принять численно равной модулю вектора 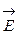, поток будет численно равен количеству силовых линий, пресекающих данную поверхность. Размерность потока в СИ: [ Ф_Е ] = В·м (вольт, умноженный на метр).

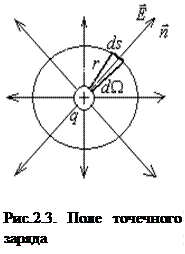Найдем поток вектора напряженности электрического поля, создаваемого точечным зарядом q, через сферическую поверхность радиуса r. Площадь ее поверхности 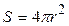. Силовые линии электрического поля, (см. рис.2.3), идут по радиусам к поверхности сферы и поэтому угол между векторам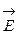и и 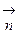равен нулю. Тогда

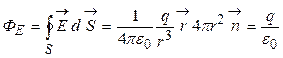. (2.1)

Можно показать, что поток через замкнутую поверхность не зависит от формы поверхности и от расположения зарядов в ней.

Далее рассмотрим поток сквозь замкнутую поверхность произвольной формы, создаваемый множеством зарядов, находящихся внутри этой поверхности. Согласно принципу суперпозиции 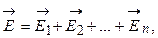поэтому

.

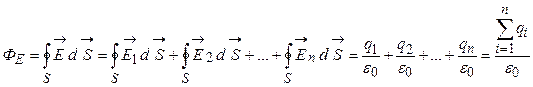Таким образом 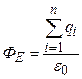. (2.2)

Тем самым, мы доказали теорему Остроградского – Гаусса: поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, охватываемых этой поверхностью, деленной на .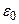

Дата добавления: 2014-01-07