К расчету электрических полей

Применение теоремы Остроградского-Гаусса

В ряде случаев теорема Гаусса позволяет найти напряженность электрического поля протяженных заряженных тел, не прибегая к вычислению громоздких интегралов. Обычно это относится к телам, чья геометрическая форма обладает определенными элементами симметрии (шар, цилиндр, плоскость). Рассмотрим некоторые примеры применения теоремы Гаусса для расчета напряженности электрических полей.

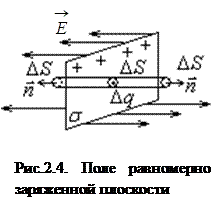Пример 1. Поле равномерно заряженной плоскости.

Электрическое поле, создаваемое бесконечно протяженной равномерно заряженной плоскостью, является однородным – в каждой точке пространства вне плоскости его напряженность всюду одинакова. Направлено это поле перпендикулярно к плоскости в обе стороны (рис.2.4). Поэтому для потока вектора напряженности поля через произвольно выбранную цилиндрическую поверхность, опирающуюся на элемент плоскости Δ S, можем написать: 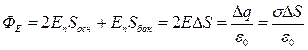, откуда 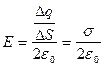, где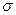- поверхностная плотность заряда. Размерность в СИ: .

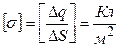Таким образом, искомая напряженность электрического поля равномерно заряженной плоскости

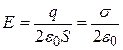. (2.3)

По этой же формуле определяется напряженность электрического поля вблизи заряженного проводника.

Пример 2. Поле между двумя бесконечно протя ж енными, разноименно заряженными параллельными плоскостями.

Вне внутреннего промежутка 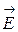= 0 т. к. поля, созданные разноименно заряженными параллельными пластинами, направлены противоположно друг другу. Между плоскостями вектора 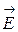, созданные зарядами каждой пластины, наоборот, направлены в одну сторону. Значит, здесь 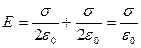. Итак:

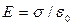. (2.4)

Пример 3. Поле равномерно заряженного цилиндра (нити).

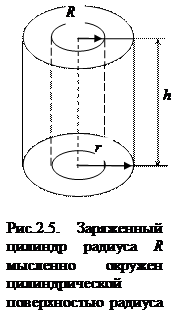
В данном случае электрическое поле, созданное цилиндром радиуса R, обладает аксиальной симметрией (т.е. симметрией относительно оси цилиндра), рис.2.5. Значит, вектора 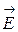направлены перпендикулярно оси цилиндра.

Заряженный цилиндр радиуса R, (см. рис.2.5), мысленно окружим коаксиальной цилиндрической поверхностью радиуса r. Поток вектора 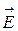через основания цилиндра равен нулю, т. к. 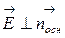, где 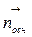– внешняя нормаль к основаниям цилиндра. Поток через боковую поверхность 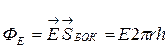, где h – высота цилиндра. Согласно теореме Остроградского – Гаусса при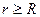 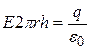. Отсюда

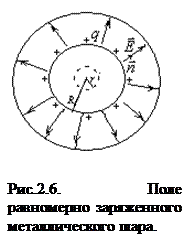
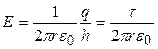. (2.5)

Здесь t = q/h – линейная плотность заряда, которая измеряется в Кл/м.

Когда r < R, 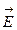= 0.

Пример 3. Поле равномерно заряженного шара.

А). Металлический шар. Окружим заряженный шар радиуса R сферической поверхностью радиуса r, рис.2.6. При равновесии заряды равномерно распределяются по внешней поверхности заряженного шара. При 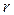<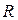(внутри шара) электрическое поле отсутствует, так как в данном случае внутри поверхности нет зарядов:

.

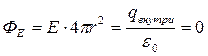
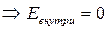Вне шара (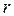>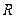) электрическое поле, созданное равномерно распределенными по его поверхности зарядами, обладает сферической симметрией (направлено по радиальным линиям), поэтому, согласно теореме Остроградского-Гаусса:

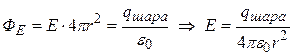. (2.6)

Видим, что электрическое поле заряженного металлического шара при 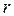>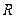не зависит от радиуса шара и совпадает с полем точечного заряда.

Б). Диэлектрический шар. Рассмотрим шар, равномерно заряженный по объему с плотностью заряда 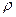(рис.2.8).

Размерность объемной плотности заряда в СИ: .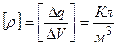

Заряд шара, очевидно, равен:

.

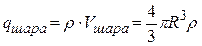Имеем по теореме Остроградского-Гаусса.

1). Внутри шара (r < R): 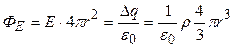, где 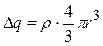- заряд внутренней области шара, ограниченной выбранной сферической поверхностью радиуса r. Отсюда находим: 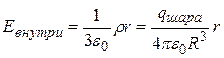. (2.7)

2). Вне шара (r > R): 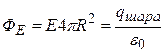, откуда

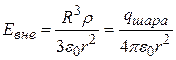, (2.8)

то есть вне заряженного диэлектрического шара электрическое поле такое же, как и в случае металлического шара.

Дата добавления: 2014-01-07