Поле сил тяготения и кулоновское силовое поле

Как видно из (2.11) и (2.16), силы гравитационного притяжения и кулоновского взаимодействия являются центральными, а поэтому соответствующие силовые поля потенциальны.

Формулам (2.11) и (2.16) можно придать единый вид

(3.27)

где

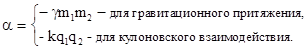
Работа силы (3.27) легко вычисляется:

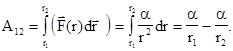(3.28)

Отсюда следует, что потенциальная энергия гравитационного взаимодействия двух материальных точек

, (3.29)

а потенциальная энергия кулоновского взаимодействия двух точечных зарядов

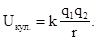(3.30)

Из (3.29) и (3.30) видно, что нулевое значение потенциальной энергии в обоих случаях соответствует бесконечно удаленным друг от друга частицам.

Поскольку гравитационное и кулоновское взаимодействие точечных объектов осуществляется посредством силовых полей, то удобно ввести понятие потенциала силового поля.

Рассмотрим это понятие на примере кулоновского поля. Если электростатическое поле создано неподвижным точечным зарядом q, и в это поле поместить другой точечный заряд q₀ (пробный заряд), то заряд q₀ в поле заряда q будет обладать потенциальной энергией

Отношение

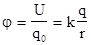
(3.31)

не зависит от свойств пробного заряда, поэтому характеризует кулоновское (электростатическое) поле заряда q и называется потенциалом поля точечного заряда.

В силу аддитивности потенциальной энергии потенциал поля 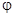, созданного системой точечных зарядов, равен алгебраической сумме потенциалов 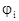, созданных в данной точке каждым из зарядов системы в отдельности, то есть

. (3.32)

Последнее соотношение является одним из математических выражений принципа суперпозиции для электростатического поля.

Используя понятие потенциала, работу по перемещению точечного заряда q в электростатическом поле можно представить в виде

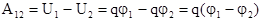, (3.33)

то есть работа сил электростатического поля по перемещению точечного заряда равна произведению заряда на разность потенциалов в начальной и конечной точках перемещения.

Отметим здесь, что аналогично можно ввести понятие потенциала гравитационного поля с соответствующими результатами.

Вывод: Кулоновское (электростатическое) и гравитационное силовые поля являются потенциальными и могут характеризоваться соответствующими потенциалами.

Дата добавления: 2014-01-07