Движение частицы в потенциальном силовом поле

Механической энергии и импульса

Полная механическая энергия системы частиц сохраняется, если на частицы системы действуют только потенциальные силы, как внутренние, так и внешние.

В тех случаях, когда на частицы системы действуют непотенциальные силы, полная механическая энергия не сохраняется, поэтому закон сохранения механической энергии не выполняется. Механическая энергия при этом переходит в другие виды энергии в равном количестве. Другими словами, ни в каких ситуациях энергия не возникает и не исчезает, она переходит из одного вида в другой.

3.8. Примеры применения законов сохранения

В механике часто встречаются задачи, в которых рассматривается движение одной частицы в потенциальном силовом поле. При этом потенциальная энергия частицы зависит от ее положения в поле 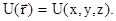Если изображать на графике зависимость потенциальной энергии от одной переменной, например от x, считая другие постоянными, то эта зависимость называется потенциальной кривой. Информация о виде потенциальной кривой позволяет получить очень ценные сведения о характере движения частицы в силовом поле, не решая уравнений ее движения.

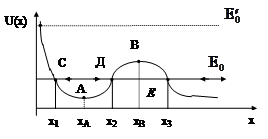
Для простоты рассмотрим одномерный случай, когда U=U(x), (рис. 3.9). Тогда из закона сохранения механической энергии следует, что

Рис. 3.9

или

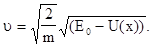(3.41)

Так как скорость частицы - действительная величина, то это условие определяет области разрешенного движения и имеет вид

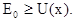(3.42)

Пусть полная механическая энергия Е₀ такова, как изображено на рис. 3.9.

Движение частицы возможно в областях: 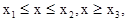для которых выполнено условие (3.42). Проанализируем более подробно результаты, следующие из (3.41) и (3.42).

1) Ограниченная область 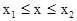называется потенциальной ямой. Движение в потенциальной яме называется финитным. В точках С и D выполняется равенство E₀=U(x), здесь скорость частицы обращается в нуль, то есть частица изменяет направление своего движения на противоположное. Координаты этих точек являются корнями уравнения E₀=U(x). Точка А соответствует минимуму потенциальной энергии (дно потенциальной ямы), здесь dU/dx|_А=0, и F=0, поэтому в этой точке находится равновесное состояние. Это состояние равновесия устойчиво, так как при сколь угодно малом отклонении от него dU/dx>0 и F направлена к положению равновесия. Таким образом, движение частицы внутри потенциальной ямы является колебательным.

2) Область x₂<x<x₃ - запрещенная область, которая называется потенциальным барьером. Здесь 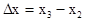- ширина потенциального барьера. Точка В - вершина потенциального барьера. В этой точке dU/dx|_B=0, поэтому частица в этой точке с энергией E=U(x_B) будет находиться в равновесии (F=0), но это равновесие неустойчиво.

3) Движение в области 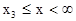инфинитно, так как происходит в неограниченной области пространства. В точке с координатой x₃ 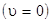происходит отражение частицы от потенциального барьера (U(x₃)=E₀).

4) Если полная энергия частицы 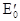больше высоты потенциального барьера, то движение инфинитно. При этом кинетическая энергия частицы максимальна в точке, где потенциальная энергия минимальна (x_А), и минимальна в точке, где потенциальная энергия максимальна (x_B).

Контрольные вопросы.

3.9. Может ли полная механическая энергия частицы принимать отрицательное значение?

3.10. Какому условию должно удовлетворять значение полной энергии тела, чтобы оно было спутником некоторой планеты?

Дата добавления: 2014-01-07