Закон сохранения механической энергии

Механической энергией называется сумма кинетической и потенциальной энергии системы частиц, то есть

E = T+U. (3.37)

Полная механическая энергия является аддитивной функцией механического состояния системы частиц, что непосредственно следует из свойств кинетической и потенциальной энергии,

Покажем, что в потенциальных силовых полях эта сумма при движении одной материальной точки остается постоянной.

Рассмотрим ситуацию, когда на частицу действуют одновременно несколько сил, среди которых есть как потенциальные, так и непотенциальные силы. В этом случае результирующую 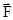всех сил можно представить как сумму результирующей потенциальных сил и результирующей непотенциальных сил :

Механическая работа силы 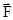при перемещении частицы

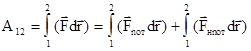
на основании (3.16) и (3.18) может быть записана в виде

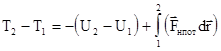
или _.

Если учесть определение (3.27), то окончательно получим

. (3.38)

Последнее соотношение называется законом превращения полной механической энергии частицы. Из него следует, что полная механическая энергия частицы может изменяться только за счет работы непотенциальных сил. С другой стороны, (3.38) означает, что работа непотенциальных сил является количественной мерой изменения полной механической энергии частицы.

Из закона (3.38) непосредственно следует закон сохранения полной механической энергии одной частицы:

Если на частицу действуют только потенциальные силы, то ее полная механическая энергия сохраняется, то есть при

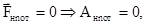поэтому Е=const. (3.39)

Законы (3.38) и (3.39) легко обобщаются на систему материальных точек. В этом случае механическая энергия включает в себя кинетическую энергию частиц системы, потенциальную энергию взаимодействия частиц между собой U_вз, а также потенциальную энергию системы во внешних потенциальных силовых полях U_внеш.:

. (3.40)

В этом общем случае закон сохранения полной механической энергии звучит так.

Дата добавления: 2014-01-07