Момент силы. Момент импульса

Рис. 3.13

Здесь рассмотрим некоторые свойства введенных в предыдущем пункте понятий момента силы и момента импульса.

Моментом силы, действующей на частицу, относительно точки названа величина (3.48)

.

Модуль и направление вектора 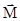определяются свойствами векторного произведения двух векторов:

- модуль вектора 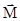численно равен площади параллелограмма, построенного на векторах и 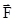, как на сторонах, то есть:

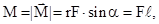(3.55)

где 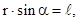- расстояние от начала отсчета О до линии, вдоль которой действует сила 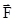, называется плечом силы;

- направление вектора момента силы 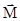определяется по правилу правого винта; вектор 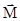направлен перпендикулярно плоскости, в которой лежат векторы и 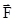, и совпадает с направлением поступательного движения правого винта при его вращении от к 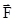кратчайшим путем. В силу условности выбора направления вектора 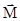момент силы является псевдовектором.

Часто необходимо знать величину проекции момента силы на некоторую ось ОZ, проходящую через точку О. В этом случае эту проекцию называют моментом силы относительно данной оси:

(3.56)

Рис. 3.14

Силу 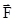можно разложить на три составляющие вдоль трех взаимоперпендикулярных направлений:

- вдоль оси ОZ - ;

- вдоль радиального R направления, перпендикулярного оси ОZ - ;

- перпендикулярно плоскости, в которой лежат ось ОZ и точка приложения силы -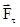, то есть

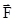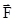= _u + + .

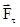Определение (3.56) примет вид

.

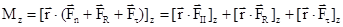Первое и второе слагаемые в правой части последнего равенства равны нулю, так как векторы и 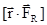перпендикулярны оси ОZ, поэтому их проекции на ось ОZ равны нулю. Теперь

(3.57)

Момент импульса относительно точки определяется таким же по форме математическим выражением, что и момент силы:

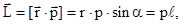(3.58)

где - -угол между векторамии ,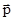

- - плечо импульса частицы относительно точки отсчета. Поэтому рассмотренные особенности вектора момента силы и его проекции на ось ОZ оказываются такими же и для вектора .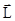

В частности,

(3.59)

- проекция момента импульса частицы относительно оси ОZ, проходящей через начало отсчета О.

Контрольные вопросы.

3.14. Определите величину момента импульса частицы m относительно точки, если скорость частицы постоянна и равна 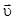, а частица мимо точки О пролетает на минимальном расстоянии r_min.

Дата добавления: 2014-01-07