Лоренцовское сокращение длины

Следствия из преобразований Лоренца

В этом пункте будут рассмотрены некоторые наиболее впечатляющие физические эффекты, существование которых можно объяснить в рамках СТО.

Сущность эффекта заключается в следующем: продольные размеры тела, движущего относительно наблюдателя, оказываются меньше, чем для наблюдателя, относительно которого это тело покоится.

Напомним, что размеры какого-либо тела определяются как разность координат его крайних точек, которые должны быть измерены в данной системе отсчета в один и тот же момент времени.

Рис. 5.4

В качестве примера рассмотрим тонкий стержень, неподвижный относительно системы 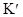и расположенный вдоль оси 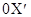(рис. 5.4).

Очевидно, что, поскольку стержень неподвижен относительно системы 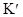, то координаты его начала 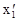и конца с течением времени остаются неизменными, поэтому требование одновременности 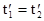их измерения в этой системе отсчета несущественно.

Длина стержня

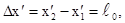(5.9)

неподвижного относительно данной системы отсчета 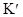, называется собственной длиной.

В системе 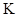, относительно которой стержень движется со скоростью 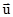, его длина

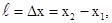(5.10)

причем координаты 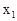и 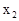должны быть измерены наблюдателем, находящимся в системе 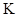, одновременно, то есть .

Используя обратные преобразования Лоренца для координат концов неподвижного относительно системы 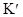стержня

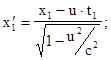
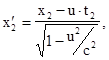
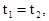
получим

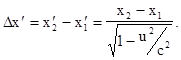
Окончательно, учтя (5.9) и (5.10), найдем, что

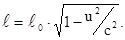(5.11)

Таким образом, действительно, длина стержня , измеренная наблюдателем, относительно которого стержень движется, оказывается меньше длины неподвижного стержня .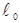

Контрольные вопросы.

5.4. Покажите, что собственная длина 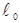является инвариантом относительно преобразований Лоренца.

5.5. Убедитесь, что поперечные размеры тела в различных инерциальных системах отсчета одинаковы.

Дата добавления: 2014-01-07