Скорость света в вакууме не зависит от относительной скорости источника света и его приемника и одинакова во всех инерциальных системах отсчета

Любое физическое явление независимо от его природы протекает одинаково во всех инерциальных системах отсчета.

Принцип относительности Эйнштейна

Это означает, что не только с помощью механических опытов (принцип относительности Галилея), но и с помощью любых опытов невозможно выделить какую-либо одну инерциальную систему отсчета, по сравнению с другой: все они совершенно равноправны. Другими словами, при переходе от одной инерциальной системы отсчета к другой вид любого физического закона остается инвариантным.

Принцип постоянства (инвариантности) скорости света

Механика, построенная на этих принципах, коренным образом изменила представления о пространстве и времени как существующих независимо от материальных объектов.

5.3. Преобразования Лоренца

Преобразования Галилея (5.1) и (5.2) противоречат опытным фактам, концентрированными выводами из которых являются постулаты СТО. А. Эйнштейн показал, что для одновременного выполнения постулатов СТО необходимо заменить преобразования Галилея другими преобразованиями, которые были получены Лоренцом раньше создания СТО.

В случае перехода от системы отсчета 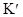к системе 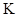(рис. 5.2) преобразования Лоренца имеют вид

(5.5)

Переход от системы 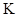к системе 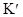осуществляется заменой в (5.5) на 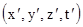и наоборот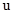, а на .

Из вида (5.5) непосредственно следует, что при преобразования Лоренца переходит в преобразования Галилея (5.2), а это означает, что механика Ньютона является предельным случаем СТО.

В соответствии с тем, что скорость света в вакууме является предельной, из (5.5) видно, что при 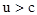формулы преобразований Лоренца теряют смысл.

Мы не будем здесь приводить прямой вывод преобразований Лоренца. В их справедливости предлагаем убедиться читателю из рассмотрения следующего примера.

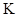Пусть в некоторый момент начала координат систем и 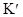совпадали. Если в этот момент в начале координат систем 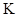и 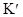точечный источник испускает короткую вспышку света, то спустя промежуток времени 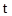в системе 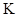свет достигнет точек, лежащих на поверхности сферы с центром в начале координат системы 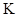и радиусом , равным , то есть

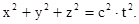(5.6)

Этот же процесс в системе 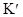будет описываться уравнением

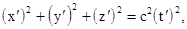(5.7)

в соответствии с принципом постоянства скорости света.

Очевидно, что преобразования координат, удовлетворяющие постулатам СТО, должны оставлять вид уравнений (5.6) и (5.7) инвариантным при переходе от одной системы отсчета 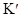к другой 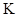и наоборот.

Непосредственной подстановкой легко убедиться, что преобразования Галилея (5.2) не удовлетворяют этим требованиям, а преобразования Лоренца оставляют инвариантными уравнения (5.6) и (5.7).

В этом пункте необходимо более подробно обсудить содержание понятия “система отсчета”. Как указывалось в 1.3.1, в понятие системы отсчета входит система координат, связанная с телом отсчета, и часы, неподвижные относительно тела отсчета. Для описания какого-либо события в данной системе отсчета необходимо знать, где относительно тела отсчета и в какой момент времени это событие происходит. На эти вопросы можно ответить, если каждой точке пространства приписать координаты путем откладывания вдоль осей координат эталонного масштаба, принятого за единицу.

Для сравнения моментов времени, в которые происходят два события в разных точках, необходимо в этих точках иметь часы, которые должны идти синхронно.

Опишем процесс синхронизации часов. Пусть в точках А и В данной системы отсчета находятся часы.

  Рис. 5.3

Из точки А в направлении В испускается световой импульс, который после отражения возвращается в точку А. Часы в А и В считаются синхронизированными, если момент испускания 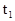светового импульса по часам А, момент его отражения 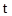по часам В и момент возврата в точку А 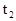по часам А связаны соотношением

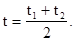(5.2)

Такую синхронизацию проводят для всех часов, находящихся в каждой точке данной системы отсчета.

Теперь можно сказать, что два события, происходящие в разных точках данной системы отсчета, одновременны, если соответствующие показания часов, находящихся в этих точках, совпадают.

В заключение этого пункта отметим, что время 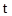и 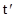, входящее в преобразования Лоренца, измеряется по часам, которые синхронизированы в системе 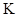и в системе 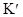, соответственно.

Контрольные вопросы.

5.2. Покажите, что преобразования Галилея являются предельным случаем преобразований Лоренца.

5.3. Убедитесь, что преобразования Лоренца удовлетворяют утверждению, что скорость света в вакууме является предельной скоростью движения материальных объектов.

Дата добавления: 2014-01-07