При решении конкретных задач

Применение основных законов динамики твердого тела

При решении конкретных задач, связанных с описанием движения твердого тела, следует помнить, что твердое тело в механике представляет собой частный случай системы материальных точек, имеющих в процессе рассматриваемого движения неизменное друг относительно друга взаимное расположение. Как уже указывалось (3.7) и (3.3), в этом случае справедливы основные уравнения динамики

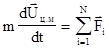(4.25)

и

. (4.26)

Из этих уравнений непосредственно видно, что характер движения твердого тела полностью определяется действующими на него внешними силами 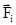и моментами этих сил .

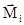Для практического применения основных уравнений (4.2) и (4.26) полезно следовать рекомендациям, упрощающим решение конкретных задач:

- Сделать схематический чертеж, на котором указать все внешние силы, действующие на рассматриваемое тело. При этом силы следует изображать в тех точках тела, на которые эти силы действуют.

- Выбрать инерциальную систему отсчета, связанную с какой-либо неподвижной или движущейся равномерно и прямолинейно точкой, относительно которой определяются моменты внешних сил. Если тело имеет неподвижную ось вращения, то полезно эту точку выбрать на неподвижной оси, а ось 0Z декартовой системы координат направить вдоль оси вращения. В случае плоского движения твердого тела ось 0Z рекомендуется направить перпендикулярно плоскости, в которой лежит траектория какой-либо точки тела.

- Точку приложения конкретной силы можно перемещать вдоль линии действия силы, так как при этом момент этой силы не изменяется. Это полезно делать при необходимости определения равнодействующей внешних сил.

- Записать уравнения (4.25) и (4.26) в проекциях на оси координат выбранной системы отсчета и, с использованием уравнений связи (например, 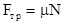) и дополнительных условий задачи, решить полученную систему уравнений относительно искомой величины.

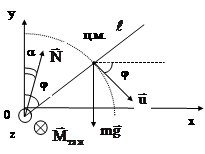
Рис. 4.6

Для примера подробно исследуем свободное вращение жесткого однородного стержня массой 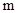и длиной 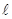в вертикальной плоскости относительно горизонтальной оси, проходящей через один из его концов (рис. 4.6). Трением в оси пренебрегаем. Выберем оси координат, как указано на рис. 4.6 (ось Z направлена из-за чертежа вдоль оси вращения стержня). При свободном вращении на стержень действуют две силы: сила тяжести 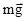и реакция оси вращения 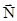. Поэтому уравнения динамики (4.25) и (4.26) примут вид

,

,

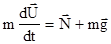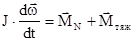где и 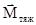- моменты сил 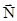и 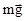соответственно. Запишем эти уравнения в проекциях на выбранные оси координат

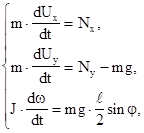
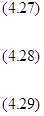
где угол 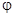отсчитывается от оси .

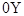В уравнении (4.29) учтено, что 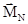относительно оси вращения равен нулю. Исследование удобнее и проще всего проводить, если перейти в уравнениях (4.27)-(4.29) от переменной 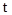к переменной 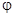. Заметим, что в этом случае 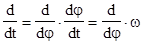, кроме этого, учтем, что 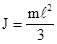относительно оси вращения, согласно (4.13). Теперь уравнения (4.27)-(4.29) примут вид:

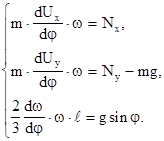
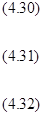
Легко заметить, что последнее равенство (4.32) эквивалентно условию

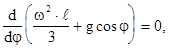
что проверяется прямым дифференцированием. Равенство нулю производной означает, что сумма в скобках при вращении стержня остается постоянной, то есть

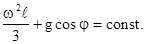
Значение константы определим, положив, например, 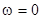при 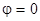, что соответствует началу вращения стержня из вертикального положения без толчка. В этом случае 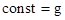, поэтому 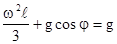, при заданных начальных условиях 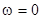. Поэтому значение угловой скорости стержня в любом его положении определяется равенством

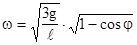. (4.33)

Используя связь (1.31), найдем теперь значения модуля скорости центра масс стержня

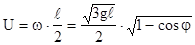, (4.34)

а затем и проекций 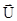на оси координат

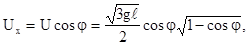(4.35)

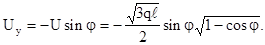(4.36)

Уравнения (4.30) и (4.31) позволяют определить проекции силы 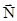, для этого необходимо, соответственно, использовать (4.35) и (4.36):

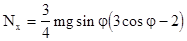, (4.37)

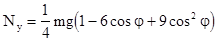. (4.38)

Интересно отметить, что при вращении сила 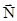, вообще говоря, не направлена вдоль стержня, а составляет с вертикалью (с осью 0Y) угол

. (3.39)

Модуль силы 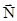равен

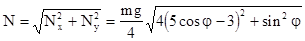(4.40)

и нигде в нуль не обращается.

Выводы: Свободное вращение стержня в вертикальной плоскости является неравномерным. Зависимости угловой скорости вращения, скорости его центра масс, а также реакции оси от положения стержня определяются формулами (4.33)-(4.40).

Контрольные вопросы.

4.9. Покажите, что равенство (4.33) является следствием из закона сохранения механической энергии стержня.

4.10. Определите, в каких положениях стержня (-?) реакция его оси направлена а) горизонтально; б) вертикально; в) вдоль стержня?

Рис. 4.7 Рис. 4.8

4.8. Понятие о прецессии

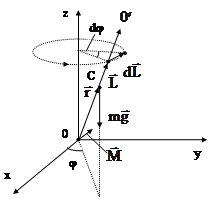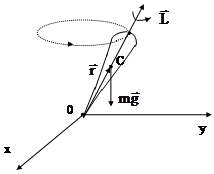
Рассмотрим здесь качественно характер движения симметричного твердого тела, имеющего одну неподвижную точку 0 (рис. 4.7), которая лежит на оси симметрии тела . В динамике вращательного движения такое тело называется гироскопом или симметричным волчком. Примером такого тела является обыкновенный детский волчок (юла). Поставим волчок на горизонтальную опору и приведем его в быстрое вращение относительно оси симметрии 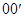, в результате волчок приобретет момент импульса 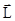, направленный вдоль оси .

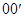Дальнейшее движение волчка будет определяться результирующим моментом сил, действующих на волчок относительно неподвижной точки 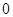, который равен

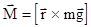
и направлен перпендикулярно плоскости (рис. 4.8). Заметим, что момент силы реакции опоры относительно точки 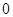равен нулю.

Из-за действия момента силы тяжести 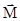, в соответствии с уравнением моментов (3.52), за время момент импульса волчка 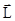получит приращение 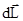, равное

.

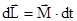Отметим, что 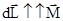, а поэтому приращение 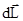направлено перпендикулярно плоскости . Таким образом, ось волчка 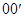за время повернется в направлении 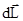на некоторый угол 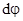. Поскольку взаимная ориентация векторов 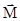, 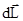и плоскости в любой момент времени остается неизменной, то ось вращения волчка 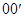будет поворачиваться относительно вертикали 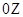, описывая конусообразную поверхность.

Подобный характер движения будет наблюдаться, когда симметричное твердое тело, имеющее одну неподвижную точку и вращающееся вокруг оси симметрии, подвержено действию постоянного по величине внешнего момента силы. При этом его ось вращения сама поворачивается относительно неподвижной оси - такое вращение называется прецессией.

Особое распространение в технике получили так называемые уравновешенные гироскопы, когда неподвижной точкой при вращении гироскопа является его центр инерции, а собственная ось вращения гироскопа может свободно поворачиваться в любом из трех взаимно перпендикулярных направлений. Таким образом, собственная ось вращения гироскопа является свободной. Это достигается с помощью так называемого карданова подвеса (рис. 4.9), в котором оси внешнего и внутреннего 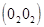колец и собственная ось гироскопа пересекаются в одной точке: центре подвеса. Уравновешенные гироскопы являются основным элементом автоматического управления в навигационных приборах движущихся объектов (самолетов, кораблей, ракет и т.д.), а также используются в приборах для измерения угловых и линейных скоростей. Действие подобных приборов основано на главном свойстве гироскопа: при любых поворотах оси внешнего кольца,

0₁

0₁

0₂

0₂

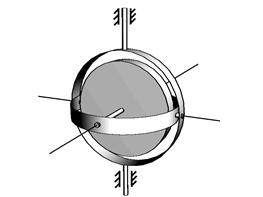
Рис. 4.9

неподвижной относительно движущегося объекта (например, самолета), собственная ось вращения гироскопа не изменяет своей ориентации в пространстве. Это свойство непосредственно следует из закона сохранения момента импульса.

Дата добавления: 2014-01-07