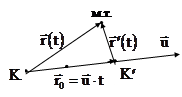Преобразования Галилея. Принцип относительности Галилея

ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ (СТО)

Как уже указывалось в п. 1.3.1, характер и вид движения материальной точки очень сильно зависит от выбора системы отсчета.

Наибольший интерес в классической механике представляют системы отсчета, в которых свободная, то есть невзаимодействующая с окружающими объектами, материальная точка движется равномерно и прямолинейно (в частности, покоится). Такие системы отсчета получили название инерциальных.

В действительности совершенно свободных тел не существует, поэтому инерциальные системы отсчета являются идеализированными физическими моделями.

Рассмотрим некоторую инерциальную систему отсчета , которую примем условно за неподвижную, и систему отсчета , которая движется относительно системы равномерно и прямолинейно со скоростью 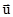. В классической механике одним из фундаментальных предположений является утверждение, что время во всех системах отсчета течет одинаково, то есть 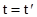. Это утверждение является следствием одной из основополагающих гипотез классической механики:

Возмущения силовых полей, несущих информацию об изменении состояния взаимодействующих тел, распространяются в пространстве мгновенно, то есть с бесконечно большой скоростью.

Положение материальной точки относительно систем отсчета 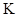и в момент времени 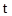будет описываться соотношением (рис.5.1)

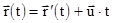, (5.1)

при условии, что при 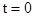начала координат систем отсчета и 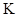совпадают.

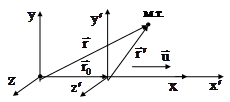
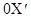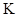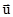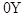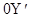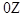Если оси координат и систем и направить вдоль , а и , и 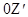параллельно друг другу соответственно (рис. 5.2), то выражение (5.1) в проекциях на оси координат систем и примет вид

Рис. 5.1

Рис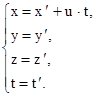. 5.2

(5.2)

Уравнения (5.1) и (5.2) называются преобразованиями Галилея и позволяют, зная состояние материальной точки в одной инерциальной системе отсчета , описывать состояние этой точки в другой инерциальной системе отсчета 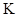и наоборот.

Отметим, что дифференцирование по времени выражения (5.1) дает классический закон сложения скоростей

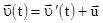. (5.3)

При дифференцировании выражения (5.3) с учетом 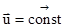получим

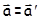. (5.4)

Из равенства (5.4) следуют два важных вывода:

1) Любая система отсчета , движущаяся относительно некоторой инерциальной системы отсчета 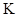равномерно и прямолинейно, также является инерциальной.

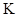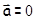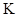Действительно, если система инерциальна, то у свободной материальной точки в этой системе , следовательно, в системе , движущейся относительно с 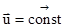, у этой материальной точки 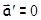(5.4). Поэтому тоже инерциальна.

2) Все инерциальные системы отсчета совершенно равноправны. Уравнения динамики при переходе от одной инерциальной системы к другой не изменяют своего вида, то есть инвариантны по отношению к преобразованиям Галилея.

Этот вывод фактически является содержанием принципа относительности Галилея.

Контрольные вопросы.

5.1. Покажите, что в рамках ньютоновской механики закон сохранения импульса инвариантен относительно преобразований Галилея.

Дата добавления: 2014-01-07