Релятивистские импульс и масса частицы

В этом и последующих пунктах будут введены основные понятия и соотношения релятивистской динамики. Необходимость пересмотра классических представлений динамики Ньютона при переходе к динамике релятивистских скоростей вытекает из следующих соображений.

Как уже указывалось в пункте 5.1, из преобразований Галилея (5.2) следует (5.4), что непосредственно свидетельствует об инвариантности второго закона Ньютона по отношению к преобразованиям Галилея.

Нетрудно показать, что в релятивистском случае связь между ускорениям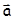и и 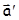в различных инерциальных системах отсчета более сложная. В частности, для 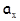и 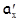она имеет вид

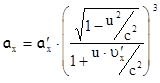. (5.19)

Это означает, что произведение 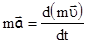с независящей от скорости массой 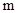не является инвариантом относительно преобразований Лоренца. Поэтому классическое определение импульса частицы для релятивистского случая требует уточнения. Можно показать, что правильное выражение для импульса частицы в релятивистском случае имеет вид

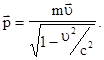(5.20)

Наиболее строго это следует из требования инвариантности закона сохранения импульса относительно преобразований Лоренца. В случае релятивистское выражение (5.20) переходит в классическое, как и должно быть, .

Если ввести понятие релятивистской массы частицы

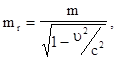(5.21)

где 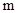- независящая от скорости (инвариантная) величина, называемая массой покоя, то формально сохраняется классический вид определения импульса .

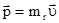Релятивистски инвариантный основной закон динамики

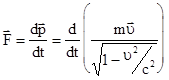(5.22)

имеет ту же форму, что и классический второй закон Ньютона, но с учетом релятивистского (5.20) выражения для импульса частицы.

Отметим, что из определения релятивистской массы (5.21) непосредственно следует, что СТО допускает движение со скоростью 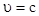только таких частиц, у которых масса покоя 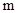равна нулю. Более того, из (5.21) видно, что такие частицы могут существовать только в единственном состоянии, двигаясь точно со скоростью .

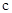Контрольные вопросы.

5.8. Докажите справедливость (5.19).

5.9. Как будут изменяться компоненты скорости 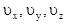релятивистской частицы, если на нее подействует сила, направленная в ту же сторону, что и ?

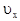Дата добавления: 2014-01-07