Понятие множества. Операции над множествами

Множество вещественных чисел.

Множество.

Введение.

Математика – одна из самых древних наук. Первые математические сведения и понятия восходят к доисторическим временам. Математика возникла на заре цивилизации как ответ на жизненно важную потребность человека в количественном отображении окружающего его мира: нужно было подсчитать расстояния, площади возделываемых полей, собранный урожай,..

Самостоятельной наука математика стала в Древней Греции примерно в VI в. до н. э. Все философские школы того времени включали того времени включали математику в круг вопросов мировоззрения: строгий язык формальной логики (именно он стал языком математики) формировал и стройное мышление. В III в. до н. э. математика выделилась из философии, что отражено в «Началах» - труде Евклида, фундаменте классической геометрии – которые служат основой для школьных учебников геометрии во всех странах в течение более 2-х тысяч лет.

Много веков после этого математика эволюционировала медленно, и только в XVII век стал эпохой ее бурного развития. Галилей и Кеплер применили математику в исследовании движения небесных тел, что привело к поразительным по тому времени открытиям – законам движения планет вокруг Солнца. Труды Декарта, Ньютона и Лейбница ознаменовали новый этап развития математики и появление математики переменных величин. Начался период дифференциации единой науки на ряд самостоятельных математических наук: математический анализ, аналитическую геометрию, алгебру. В свою очередь, это инициировало интенсивное развитие физики и астрономии.

Современная математика интенсивно проникает в другие науки. Язык математики уникален, что является объективным отражением универсальности законов окружающего нас многообразного мира.

Экономика как наука об объективных причинах функционирования и развития общества еще со Средних веков пользуется разнообразными количественными характеристиками, а потому вобрала в себя большое число математических методов. Так, современный бухгалтерский учет основан на принципах, изложенных еще в 1494 г. В фундаментальном труде Луки Пачали «Сумма арифметики, геометрии, учения о пропорциях и отношениях», в котором часть I, отдел 9, представляет собой трактат XI «О счетах и записях».

Современная экономика использует методы, разработанные в XX в. Л. В. Канторовичем, В. В. Леонтьевым, Е. Е. Слуцким. В это же время интенсивно развивался и математический аппарат, применяемый в экономике.

Понятие множества является одним из основных неопределяемых понятий математики. Под множеством понимают некоторую совокупность объектов, рассматриваемую как единое целое. Объекты, из которых состоит множество, называются его элементами. Множества принято обозначать большими латинскими буквами, а его элементы – малыми. Если элемент х принадлежит множеству Х, то пишут « ».

Существуют несколько способов записи множества:

- перечислительный

;

- с помощью характеристического свойства:

.

Определение. Множество, не содержащее ни одного элемента, называется пустым.

Определение. Множество 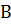называется подмножеством множества 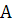, если каждый элемент множества 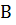принадлежит множеству .

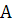Обозначение: .

Определение. Множества 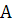и 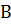называются равными, если и .

Обозначение: .

Определение. Если и , то 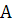называется собственным подмножеством множества .

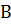Обозначение: .

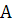Определение. Пересечением множеств и 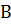называется множество , состоящее из всех элементов, принадлежащих как множеству 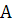, так и множеству .

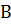Обозначение: .

=

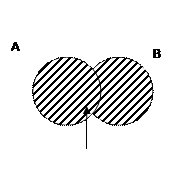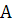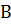Определение. Объединением множеств и называется множество , состоящее из всех элементов, принадлежащих либо множеству 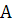, либо множеству .

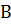Обозначение:

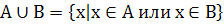
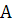Определение. Разностью множеств и 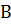называется множество , состоящее из всех элементов, принадлежащих множеству 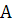и не принадлежащих множеству .

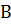Обозначение: .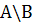

А\В={x | xÎА и xÏВ}

Обозначения: «противоречие» - ↯

«для любого» -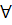

«тогда и только тогда, когда…» -

«такое, что» -:

«единственность» -!

Определение. Множество, содержащее конечное число элементов, называется конечным. В противном случае – бесконечным.

Определение. Множество с заданным порядком следования элементов называется упорядоченным.

Дата добавления: 2014-01-07