Числовые множества

Множество действительных (вещественных) чисел.

Определение. Множества, элементами которых являются числа, называются числовыми.

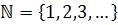- множество натуральных чисел;

- множество целых чисел;

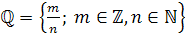- множество рациональных чисел;

- множество действительных чисел.

Замечание: Между множествами ℕ, ℤ, ℚ, ℝ существует соотношение:

.

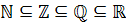Множество ℝ разбивается на два множества: ℚ и множество иррациональных чисел. Действительные числа, не являющиеся рациональными, называются иррациональными.

Теорема 1. Не существует рационального числа, квадрат которого равен числу 2.

Свойства множества ℝ:

1°. Множество ℝ является упорядоченным, т. е. .

2°. Множество ℝ плотное, т. е. между любыми двумя различными числами a и b содержится бесконечное множество действительных чисел х.

3°. Множество ℝ непрерывное.

Пусть множество ℝ разбито на два непустых класса A и B такие, что каждое действительное число содержится только в одном из них и 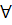a∈A, b∈B выполнено a < b. Тогда (свойство непрерывности) существует единственное число c∈ℝ: a ≤ c ≤ b 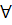a∈A, b∈B. Оно отделяет числа класса A от чисел класса B. Число c называется либо наибольшим числом в классе A (тогда в B нет наименьшего числа), либо наименьшего в классе B (тогда в A нет наибольшего числа).

Свойство непрерывности позволяет установить взаимно-однозначное соответствие между множеством ℝ и множеством всех точек прямой. Это означает, что 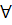x∈ℝ соответствует определённая единственная точка числовой оси, и наоборот, 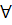точке прямой соответствует определённое единственное действительное число.

Пусть a,b ∈ℝ, a < b. Будем использовать следующие обозначения:

1) [a,b]={x∈ℝ|a ≤ x ≤ b} – отрезок (сегмент);

2) (a,b)={x∈ℝ|a < x < b} – интервал;

3) ℝ=(-∞;˖∞);

4) [a;b), (a;b], (a;˖∞), [a;˖∞), (-∞;a), (-∞;a] – аналогично.

Определение. Пусть x_₀∈ℝ. Окрестностью точки x_₀ называется любой интервал (a,b), содержащий точку x_₀. В частности интервал 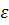(x_₀- ,x_₀˖ 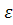), где 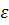> 0, называется -окрестность точки x_₀.

Дата добавления: 2014-01-07