
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение и свойства
|
|
|
|
Производная функции.
К понятию производной приводит задача о вычислении мгновенной скорости движущейся материальной точки, задача о вычислении скорости изменения стоимости акций, задача о касательной к кривой и другие задачи.
Определение. Пусть функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки 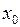 . Производной функции называется
. Производной функции называется
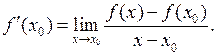 (1)
(1)
Если предел в (1) существует, то функция  называется дифференцируемой в точке
называется дифференцируемой в точке 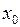 . В противном случае говорят, что функция
. В противном случае говорят, что функция  не имеет производной в точке
не имеет производной в точке 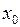 или не дифференцируема точке
или не дифференцируема точке 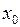 .
.
Для обозначения производной используются также символы:
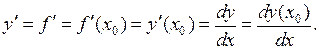
Обозначим  и
и  называются приращениями аргумента и функции соответственно. Тогда
называются приращениями аргумента и функции соответственно. Тогда 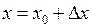 и
и  при
при  . Поэтому равенство (1) можно переписать так:
. Поэтому равенство (1) можно переписать так:
 .
.
Определение. Функция  называется дифференцируемой на промежутке
называется дифференцируемой на промежутке 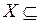 R, если она дифференцируема в каждой точке этого промежутка.
R, если она дифференцируема в каждой точке этого промежутка.
Сформулируем основные правила дифференцирования.
Пусть 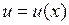 и
и 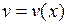 дифференцируемые в точке
дифференцируемые в точке 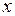 функции и
функции и 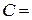 const. Тогда
const. Тогда
 (производная константы равна 0);
(производная константы равна 0);

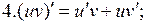
 ;
; 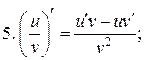
 Правило дифференцирования сложной функции.
Правило дифференцирования сложной функции.
Пусть функция 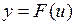 дифференцируема в точке
дифференцируема в точке 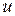 , а функция
, а функция  дифференцируема в точке
дифференцируема в точке 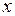 .Тогда сложная функция
.Тогда сложная функция 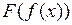 дифференцируема в точке
дифференцируема в точке 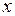 и
и
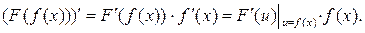
Таким образом, производная сложной функции равна произведению производной внешней функции на производную внутренней функции.
Приведем таблицу производных основных элементарных функций.
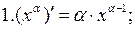 8.
8. tg
tg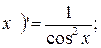

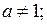
 9.
9. ctg
ctg
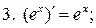



 12.
12. arctg
arctg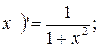
 13.
13. arcctg
arcctg

Формулы 1. – 9. данной таблицы получаются из таблицы пределов с помощью правил 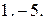 Например,
Например, 
 Здесь мы использовали формулу (2) и правило 4.
Здесь мы использовали формулу (2) и правило 4.
Используя правила дифференцирования 1.- 6. и таблицу производных можно найти производную любой элементарной функции.
Пример 1.

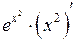
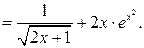
Пример 2. Пусть  . Найти
. Найти  . Выделим у этой сложной функции внешнюю и внутреннюю функции:
. Выделим у этой сложной функции внешнюю и внутреннюю функции: 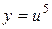 , где
, где 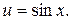
Пользуясь правилом 6, найдем
 .
.
Замечание 1. Из предыдущего примера видно, как важно при вычислении производной сложной функции правильно выделить внешнюю и внутреннюю функции.
Замечание 2. Если функция  дифференцируема в точке
дифференцируема в точке  , то
, то  непрерывна в точке
непрерывна в точке  . Действительно,
. Действительно, 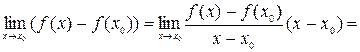
 Обратное неверно. То есть дифференцируемая в точке
Обратное неверно. То есть дифференцируемая в точке  функция может не иметь производной в точке
функция может не иметь производной в точке  . Например, функция
. Например, функция 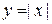 непрерывна при всех
непрерывна при всех 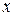 , но не дифференцируема при
, но не дифференцируема при 
Задача. Доказать, что функция 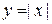 не дифференцируема при
не дифференцируема при 
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 277; Нарушение авторских прав?; Мы поможем в написании вашей работы!