Расчет доверительного интервала для математического ожидания

Ошибка среднего квадратического отклонения

Показатель точности среднего значения

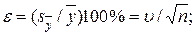(2.10)

(2.11)

Величина 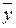, найденная по выборке, представляет ценность постольку, поскольку по ней можно судить об истинном среднем, математическом ожидании 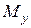. Представляет интерес отыскание величины максимальной ошибки , которую мы допускаем, предполагая 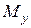равным 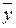. Требуется, следовательно, найти величину при которой

(2.12)

Неравенством (2.12) задается интервал, в котором находится значение математического ожидания 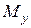. Этот интервал называется доверительным интервалом для математического ожидания. Величина зависит от объема выборки 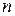. Чем больше 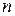, тем меньше максимальная ошибка . Однако, даже при заданном 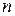нельзя абсолютно достоверно указать величину , так как расчет этой величины, как и любой статистический вывод, делают на основе результатов эксперимента, а они заведомо содержат ошибки. Выводы, которые делают на основе неточных данных, принципиально не могут быть абсолютно достоверными. Поэтому говорят о надежности статистического вывода, которую оценивают величиной доверительной вероятности 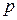, где 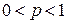. Например, статистический вывод, сделанный с доверительной вероятностью 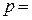0,95, будет справедлив в 95 случаях из 100. Будем пользоваться чаще величиной 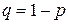, называемой уровнем значимости. Уровень значимости задается заранее, до проведения расчетов. Типичные значения для 0,01; 0,05 и 0,1 или, в процентах: 1, 5, 10.

Вернемся к отысканию доверительного интервала для математического ожидания. Будем предполагать, что дисперсия измеряемой величины 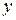заранее неизвестна, а ее оценка 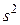найдена по выборке с помощью формул (2.5) или (2.7). В этом случае величина определяется по формуле 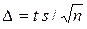, следовательно, доверительный интервал для математического ожидания равен

(2.13)

Величина 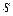– это оценка стандарта. Кроме известных величин 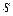и 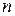в формулу (2.13) входит величина 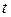, для отыскания которой понадобятся статистические таблицы. Они имеются практически в каждом руководстве по математической статистике или планированию эксперимента.

Величина 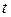называется табличным значением 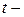критерия Стьюдента. В соответствующей таблице ее следует выбирать по предварительно заданному уровню значимости 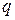и числу степеней свободы .

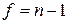Оценку для математического ожидания в виде интервала (2.13) часто называют интервальной оценкой в отличие от оценки по формуле (2.4), которую называют точечной оценкой для математического ожидания.

Не следует думать, что во всех случаях целесообразно задаваться возможно большей надежностью статистического вывода. С большей надежностью можно гарантировать только более широкий доверительный интервал для математического ожидания при тех же опытных данных.

Дата добавления: 2014-01-07