Определение необходимого объема выборки

Пусть требуется найти минимальное число 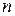повторений опытов, при котором среднее арифметическое 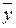, найденное по этой выборке, отличалось бы от математического ожидания не более чем на заданную величину . Это, по существу, задача, обратная предыдущей. Для ее решения необходимо знать оценку дисперсии 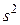. Здесь можно использовать, например, результаты проведенных ранее исследований (разведывательных опытов). Искомое значение 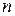определяется по формуле

(2.14)

При проведении экспериментальных исследований необходимое число наблюдений в опыте определяют по формуле

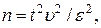
где 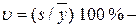коэффициент вариации (определяется по результатам проведенных ранее исследований), %;

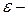показатель точности, %.

Обычно показатель точности 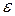принимают равным 5 %. Величину уровня значимости 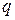выбирают равной 0,05, при этом 1,96 или 0,01 и 2,58.

При статистической обработке данных широко используют процедуры проверки статистических гипотез. Статистическая гипотеза – это некоторое предположение относительно свойств генеральной совокупности, проверяемое по выборке. Например, гипотеза об однородности средних или дисперсий, законе распределения и т. д. Проверка статистической гипотезы – это процедура, по результатам которой гипотеза принимается или отбрасывается.

Проверка статистических гипотез связана с такими распространенными задачами, как сравнительная оценка различных технологических процессов по их производительности, точности, экономичности или сравнение конструктивных особенностей машин и приборов. В планировании эксперимента проверка статистических гипотез позволяет правильно оценить преимущества одной модели перед другой, выявить наиболее значимые факторы, влияющие на данное явление, а также убедиться в пригодности (адекватности) полученного математического описания процесса.

Выдвинутую гипотезу называют основной, или нулевой. Гипотезу, противоречащую нулевой, называют конкурирующей. Для проверки нулевой гипотезы используют специально подобранную случайную величину, распределение которой известно. Ее называют статистическим критерием. Например, при проверке гипотезы об однородности дисперсий в качестве критерия используют отношение выборочных дисперсий, которое подчиняется статистическому распределению Фишера. Для проверки статистической гипотезы вычисляют значения критерия по имеющимся опытным данным. Если оно находится внутри некоторой заданной заранее области, называемой областью принятия гипотезы (областью допустимых значений), то нулевая гипотеза принимается. В противоположном случае значение критерия попадает в критическую область, и тогда гипотеза отвергается.

Однако попадание критерия в область допустимых значений не дает права категорически утверждать, что гипотеза полностью подтвердилась. Можно только заключить, что по данным выборки значение критерия не противоречит гипотезе. Поэтому, принимая решение о правильности гипотезы, можно допустить ошибку. Ошибка первого рода состоит в том, что отвергается гипотеза, которая на самом деле верна. Вероятность этой ошибки задается заранее выбором уровня значимости 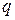. (Как указывалось, типичные значения 0,01; 0,05; 0,1 или 1, 5 и 10%.) Ошибка второго рода состоит в том, что гипотеза принимается, а на самом деле она неверна. Уменьшение ошибки второго рода достигается увеличением уровня значимости. Таким образом, уменьшение уровня значимости приводит к уменьшению ошибки первого рода и при этом к увеличению ошибки второго рода. Необходимо отметить, что единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объема выборок.

Дата добавления: 2014-01-07