Проверка гипотезы об однородности двух дисперсий

Результаты экспериментальных исследований часто используют, например, для сравнения условий функционирования объектов, оценки сравнительной эффективности различных технологий, разных способов измерения и т. д. Во многих случаях соответствующие выводы делают на основе анализа и сравнения нескольких выборок. Одна из простых задач такого типа возникает, когда надо сравнивать точность двух измерительных приборов. В этом случае, очевидно, следует сравнить оценки дисперсий соответствующих выборок.

Пусть имеются две выборки объемом 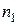и , по которым найдены выборочные дисперсии и 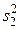. Они являются оценками для генеральных дисперсий соответственно и 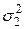. Предположим, что . Требуется выяснить, можно ли утверждать, что обе выборки взяты из одной и той же генеральной совокупности. Ее это так, то . В этом случае выборочные дисперсии и 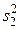называются однородными, а различие между ними объясняется влиянием случайных ошибок. В противном случае генеральные дисперсии и 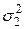не равны друг другу. Тогда говорят, что различие между выборочными дисперсиями значимо.

Для проверки статистической гипотезы об однородности двух дисперсий используется 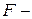критерий Фишера. Вначале вычисляется величина , равная отношению большей из выборочных дисперсий к меньшей. Пусть .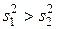

Тогда

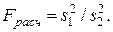(2.15)

Далее задаются уровнем значимости 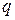и вычисляют числа степеней свободы дисперсий числителя и знаменателя по формуле (5): и 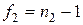. По трем величинам 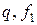и таблиц распределения Фишера отыскивают величину 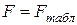. Если 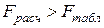, то выборочные дисперсии считаются неоднородными (различие между ними значимо) для выбранного уровня значимости 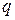. Если , то можно принять гипотезу об однородности дисперсий.

Дата добавления: 2014-01-07