Дисперсия воспроизводимости

Статистический анализ уравнения регрессии

После того как уравнение регрессии получено, приступают к его статистическому анализу. При этом решить задачу проверки адекватности математической модели. Для выполнения этой процедуры необходимо иметь количественную оценку ошибок эксперимента в целом. Соответствующей характеристикой является дисперсия воспроизводимости, обозначаемая через 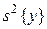. Рассмотрим способы ее вычисления в зависимости от методики дублирования опытов.

1. Равномерное дублирование. Каждый из 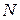запланированных опытов повторяется одинаковое число 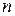раз, т. е. имеется 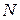серий, в каждой из которых ставится 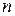дублированных опытов.

Обозначим результаты опытов первой серии через 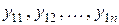. По ним можно рассчитать дисперсию первого опыта

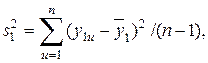(3.8)

где 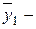среднее по серии дублированных опытов, равное

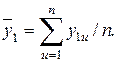(3.9)

Аналогично рассчитываются средние 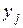и дисперсии 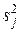всех остальных опытов:

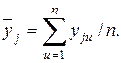(3.10)

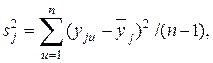(3.11)

Отметим, что числа степеней свободы всех дисперсий одинаковы и равны 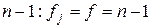. В качестве дисперсии воспроизводимости 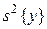берется среднее арифметическое дисперсий опытов

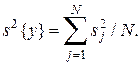(3.12)

Число степеней свободы 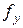этой дисперсии равно сумме чисел степеней свободы дисперсий опытов

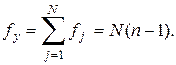(3.13)

Необходимыми предпосылками статистического анализа являются нормальность распределения выходной величины и однородность дисперсий опытов. Проверка однородности дисперсий опытов при равномерном их дублировании проводится по критерию Кохрена.

2. Неравномерное дублирование. Каждый 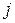-й опыт повторяется в этом случае некоторое число 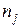раз. Как и в предыдущем случае, вычисляются дисперсии первого, второго, …, 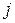-го опытов: 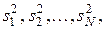по формулам, аналогичным формуле (3.11), только вместо 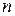здесь будет стоять :

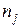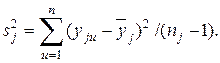(3.14)

Числа степени свободы дисперсий, вообще говоря, различны: 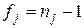. Дисперсия воспроизводимости для этого случая определяется по формуле

(3.15)

Число степеней свободы ее равно

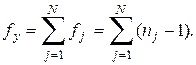(3.16)

Для проверки однородности дисперсий в данном случае необходимо воспользоваться критерием Бартлетта.

3. Рассмотрим частный случай неравномерного дублирования, когда из 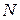поставленных опытов дублируется только один, для определенности – первый с числом повторений 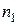раз. Дисперсия, рассчитанная по этой серии, принимается за оценку дисперсии воспроизводимости с числом степеней свободы .

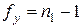4. Отсутствие дублированных опытов. Для оценки дисперсии воспроизводимости в этом случае приходится ставить отдельную серию дублированных опытов, если это возможно. Как и в предыдущем случае, дисперсия опытов этой серии служит оценкой дисперсии воспроизводимости с числом степеней свободы, равным 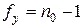, где 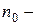число дублированных опытов в отдельной серии.

Дата добавления: 2014-01-07