Основные понятия структурного синтеза и анализа

Подвижность механизма - число независимых обобщенных координат, однозначно определяющее положение звеньев механизма на плоскости или в пространстве.
Связь - ограничение, наложенное на перемещение тела по данной координате.
Избыточные (пассивные) - такие связи в механизме, которые повторяют или дублируют связи, уже имеющиеся по данной координате, и поэтому не изменяющие реальной подвижности механизма. При этом расчетная подвижность механизма уменьшается, а степень его статической неопределимости увеличивается. Иногда используется иное определение: Избыточные связи - это связи, число которых в механизме определяется разностью между суммарным числом связей, наложенных кинематическими парами, и суммой степеней подвижности всех звеньев, местных подвижностей и заданной (требуемой) подвижностью механизма в целом. Местные подвижности - подвижности механизма, которые не оказывают влияния на его функцию положения (и передаточные функции), а введены в механизм с другими целями (например, подвижность ролика в кулачковом механизме обеспечивает замену в высшей паре трения скольжения трением качения).

Избыточные связи и лишние степени свободы (местные подвижности).

При выводе формулы Сомова Малышева предполагалось, что все уравнения связи независимы, т. е. ни одно из них не может быть получено как следствие других. В некоторых механизмах это условие не выполняется. Обозначим через q число повторяющихся (или зависимых) уравнений связи. Тогда число независимых уравнений связи равно

5× p_V+4× p_IV+3× p_III+2× p_II+ p_I- q

и число степеней свободы механизма

W =6×n -5× p_V-4× p_IV-3× p_III-2× p_II×- p_I+q

В дальнейшем повторяющиеся связи будем называть избыточными или пассивными, так как их можно удалить, сохранив при этом заданное число степеней свободы механизма. Уравнение содержит две неизвестные величины ( W и q ), так как число избыточных связей в общем случае можно определить лишь путем анализа уравнений связи. Однако в некоторых простейших случаях величина W может быть получена из непосредственного решения задачи о положениях звеньев механизма. Тогда из последнего уравнения находим число избыточных связей:

q = W+5× p_V+4× p_IV+3× p_III+2× p_II+ p_I- 6×n

Устранение избыточных связей выполняется изменением подвижностей отдельных кинематических пар, причем для одного и того же механизма с избыточными связями можно найти несколько вариантов механизма без избыточных связей. Наличие избыточных связей в механизмах ответственного назначения требует повышенной точности изготовления элементов кинематических пар во избежание дополнительных нагрузок на звенья механизма из-за их деформации, которые приводят к износу или заклиниванию с этой точки зрения избыточные связи вредны.

Рассмотрим, кривошипно-ползунный механизм, преобразующий вращательное движение в поступательное или наоборот, часто используется. В нем применимы пары с поверхностным контактом. Он прост по устройству и подходит для передачи больших усилий. На плоской схеме, независимо от классов КП, механизм не имеет избыточных связей.

W = 3×n - 2×p_н - p_в = 3×3 – 2×3 – 0 =1 и q = W+ 2× p₂ + p₁ - 3×n=0

По формуле Сомова Малышева

W =6×n -5× p₅ - 4× p₄ - 3× p₃ - 2× p₂ - p₁+q =6×3 - 5×4 – 0 – 0 – 0 + q = -2 + q,

При этом подвижность механизма, равная числу обобщенных координат W = 1, таким образом, q = W+ 2 = 3. Это означает, что при неточностях изготовления в последней паре возникнут натяги трех видов. Эти избыточные связи требуют большой точности изготовления и сборки механизма, что особенно ощутимо при увеличении размеров механизма. Условие отсутствия избыточных связей получим, подставив в исходную формулу необходимую подвижность W =1 и q = 0, учитывая, что пары I и II классов в таких механизмах не применяются, окончательно получим:

1 =6×3 -5× p_V - 4× p_IV - 3× p_III + 0,

5× p_V + 4× p_IV + 3× p_III = 17

Для создания рационального механизма – механизма, не имеющего лишних степеней свободы и избыточных связей, в кривошипно-ползунном механизме обычно применяются сферические и цилиндрические пары. Например, рациональная схема будет получена, если шатунную пару B выполнить в виде сферического шарнира, а пару С - в виде цилиндрического шарнира. Тогда

W =6×n -5× p_V - 4× p_IV - 3× p_III +q =6×3 - 5×2 – 4×1 –3×1 – 0 + q = 1 и q = 0

Однако, чем выше подвижность КП, тем дороже ее изготовление, поэтому при проектировании необходимо учесть также условия эксплуатации каждого механизма.

Таким образом, очевидно, что избыточные связи – результат введения дополнительных связей, дополнительных звеньев и занижения класса КП.

Иногда избыточные связи умышленно вводят в состав механизма для повышения его жесткости или для устранения неопределенности движения звеньев в некоторых положениях.

Так, например, коленчатый вал четырехцилиндрового двигателя образует с подшипником А одноподвижную вращательную пару, что вполне достаточно с точки зрения кинематики данного механизма с одной степенью свободы (W= 1). Однако, учитывая большую длину вала и значительные силы, нагружающие коленчатый вал, приходится добавлять еще два подшипника А' и А", иначе система будет неработоспособной из-за недостаточной прочности и жесткости. Если эти вращательные пары двухподвижные цилиндрические (так как они не должны работать в осевом перемещении), то помимо пяти основных связей будет наложено 8 добавочных (повторных) связей (q = 4× p₄ = 4× 2= 8); при этом потребуется высокая точность изготовления для обеспече­ния соосности всех трех опор, иначе вал будет силь­но деформироваться, и в ма­териале вала и подшипников могут появиться недопусти­мо большие напряжения.

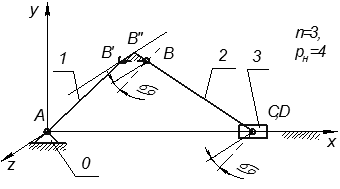
Для устранения неопределенности движения звеньев вводится дополнительное звено в так называемый спарник тепловоза, механизм сдвоенного параллелограмма. В данном механизме имеются соотношения: AB = CD, ВС = AD (т. е. фигура ABCD - параллелограмм). Где AB и CD – кривошипы. При повороте возможно возникновение так называемого вырожденного параллелограмма, т.е. кривошип AB пройдет горизонтальное положение, а CD нет. Для исключения появления такой неопределенности движения вводят дополнительное звено при этом AE = FD, EF =AD (т.е. фигура AEFD - тоже параллелограмм). По свойству параллелограмма расстояние между точками Е и F всегда равно отрезку AD, если эти точки находятся на равных расстояниях от точек А и D. Поэтому введение дополнительного звена EF при ус­ловии, что EF =AD, не вносит новых геометрических связей, и число степеней свободы остается равным 1, хотя по формуле Чебышева П.И.

W = 3×n - 2×p_н - p_в = 3×4 – 2×6 – 0 = 0

Если точность выполнения указанных геометрических соотно­шений окажется недостаточной, например, AE≠FD, то расстояние EF уже не будет равно AD, и движение станет невозможным, т. е. число степеней свободы действительно будет равно нулю.

Лишние степени свободы (местные подвижности). Вводятся конструктором для улучшения эксплуатационных свойств механизма.

В кулачковом механизме вращение ролика не влияет на закон движения толкателя и как следствие является лишней подвижностью данного механизма.

Однако, с точки зрения улучшения эксплуатационных свойств ролик вводят для замены терния скольжения толкателя трением качения ролика по кулачку, что уменьшает износ и увеличивает срок службы изделия в целом.

При изучении движения механизмов необходимо исключать избыточные связи и лишние степени свободы.

Замена высшей кинематической пары низшими

Как было показано ранее плоские механизмы могут иметь звенья входящие как в высшие, так и в низшие КП. При изучении кинематики и структуры плоских механизмов удобно заменять высшие КП кинематическими цепями или звеньями входящими только в низшие вращательные и поступательные пары V класса. При этой замене должно выполняться следующее условие: механизм, полученный после такой замены должен обладать прежней степенью свободы, а также необходимо, чтобы сохранились относительно рассматриваемого положения, движения всех его звеньев. Т.е. заменяемый и заменяющий механизм должны быть кинематически эквивалентны.

Порядок замены:

1. Провести нормаль к профилям через точку контакта
2. Найти на нормали положения центров кривизны профилей.
3. Поместить в эти точки вращательные пары V класса и соединить их дополнительным звеном.

Рассмотрим замену на примере кулачкового механизма.

Механизм обладает лишними степенями свободы – это вращение ролика вокруг оси B. Устранив возможность такого вращения, мы не изменим характера движения механизма в целом. После устранения ролика лишние степени свободы отсутствуют. Произведем замену высшей КП низшими. Для замены пары II класса проведем через точку D касания звеньев нормаль к профилю кулачка и найдем на ней центр кривизны этого профиля - точку А. Помещаем в точки А и В вращательные пары V класса и соединим эти точки условным звеном AB. Таким образом, мы получили заменяющий механизм для кулачкового механизма с качающимся толкателем – шарнирный четырехзвенник.

Структурная классификация механизмов по Ассуру Л.В.

Для решения задач синтеза и анализа сложных рычажных механизмов профессором Петербургского университета Ассуром Л.В. была предложена оригинальная структурная классификация. По этой классификации механизмы, не имеющие избыточных связей и местных подвижностей, состоят из первичных механизмов и структурных групп Ассура.

Т.е. Если плоский механизм не имеет избыточных связей, лишних степеней свободы и не содержит высших кинематических пар, то его можно построить путем присоединения к одному или нескольким механизмам первого класса одной или нескольких структурных групп. Подвижность механизма при этом равна числу механизмов I класса.

Под первичным механизмом понимают однозвенный механизм, образующий низшую кинематическую пару со стойкой (ведущее звено).

W = 3×n - 2×p_н = 3×1 – 2×1 = 1

Структурной группой Ассура (или группой нулевой подвижности) называется незамкнутая кинематическая цепь, которая, будучи замкнута на стойку, превращается в ферму.

W = 3×n - 2×p_н = 0,

Откуда можно найти связь между числом подвижных звеньев и числом низших КП структурной группы:

3×n = 2×p_н , n=2/3×p_н

pн					…
n					…

Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет свободный элемент звена, называются поводками.

Группы могут быть различной степени сложности. Структурные группы Ассура делятся на классы в зависимости от числа внутренних КП, кроме групп II класса. В пределах класса (по Ассуру) группы подразделяются по числу поводков на порядки (порядок группы равен числу ее поводков).

Механизмы классифицируются по степени сложности групп входящих в их состав. Класс и порядок механизма определяется классом и порядком наиболее сложной из входящих в него групп.

Особенность структурных групп Ассура - их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая ферма. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов. Для этих групп разработаны типовые методы структурного, кинематического и силового анализа (например, программа DIADA). Структурному анализу по Ассуру можно подвергать только механизмы, не содержащие избыточных связей и подвижностей. Поэтому перед проведением структурного анализа необходимо устранить избыточные связи и выявить местные подвижности. Затем необходимо: выбрать первичные механизмы и, начиная со звеньев наиболее удаленных от первичных, выделять из состава механизма структурные группы нулевой подвижности. При этом необходимо следить, чтобы звенья, остающиеся в механизме, не теряли связи с первичными механизмами.

При структурном синтезе механизма по Ассуру к выбранным первичным механизмам с заданной подвижностью W₀ последовательно присоединяются структурные группы c нулевой подвижностью. Полученный таким образом механизм обладает рациональной структурой, т.е. не содержит избыточных связей и подвижностей.

Порядок проведения структурного анализа по Асуру:

1. Изобразить структурную схему механизма.

2. Пронумеровать подвижные звенья, начиная с ведущего.

3. Буквами обозначить КП.

4. Вычислить подвижность, избавится от избыточных подвижностей и лишних степеней свободы.

5. При необходимости, заменить высшие КП низшими.

6. Расчленить механизм на структурные группы.

Правило: Расчленение механизма на структурные группы начинают с отсоединения структурной группы наиболее удаленной от ведущего звена.

7. Написать структурную формулу механизма.

Дата добавления: 2014-01-07