Обобщенное уравнение состояния

Матричная запись уравнений состояния электрической системы

Под уравнением состояния понимается матричное уравнение (система уравнений), которое описывает режимы работы электрической системы.

В зависимости от того, что при расчете установившегося режима принимается за исходные и независимые параметры. Выделяются три вида матричных уравнений состояния:

1.обобщенное уравнение состояния;

2.уравнение узловых напряжений;

3.уравнение контурных токов.

Обобщенное уравнение состояния получается за счет объединения матричных уравнений I и II законов Кирхгофа. Это позволяет, получить число независимых уравнений в соответствующей системе уравнений, равные числу независимых токов в ветвях. Общий вид уравнения не зависит от конфигурации схемы и числа ее элементов.

M · I = J – I закон Кирхгофа

N Z_BI = Е_К – II закон Кирхгофа

Матрицы М и N Z_B будем рассматривать как блоки единой матрицы коэффициентов

А = 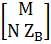– матрица параметров схемы замещения

Матрицы J и Е_К представляются как блоки объединенной матрицы исходных параметров:

F =

Тогда обобщенное уравнение в матричной форме имеет вид:

А · I = F

Структура:

Составить обобщенное уравнение состояния для расчетной схемы (в общем виде), если известны сопротивления ветвей Z₁, Z₂, Z₃, Z₄, Z₅ и задающие токи J₁, J₂, J₃

1 2 3 4 5

М =

- - - - -

Б 1 0 0 0 -1

1 2 3 4 5

N =

J = - задающие токи берутся положительными для генераторных узлов и отрицательными для нагрузочных узлов.

Е_к == - так как отсутствуют ЭДС в ветвях схемы.

Находим произведение N Z_B

N Z_B = . = =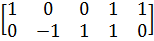

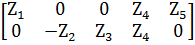
Обобщенное уравнение состояния имеет вид:

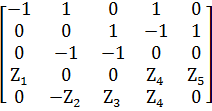. (1.5)

A · I = F

Перейдем к системе уравнений:

- I₁ + I₂ + I₄ = J₁

I₃ – I₄ + I₅ = J₂

- I₂ – I₃ = J₃ (1.6)

Z₁ I₁ + Z₄ I₄ + Z₅ I₅ = 0

-Z₂ I₂ + Z₃ I₃ + Z₄ I₄ = 0

Используя обобщенное уравнение состояния, порядок расчета установившегося режима можно свести к следующему:

1.определяются токи в ветвях схемы по одному из возможных способов:

а)решается матричное уравнение (1.5)

I = A^-1 F

б)находятся корни системы уравнений (1.6)

2.рассчитываются падения напряжений в ветвях схемы на основе закона Ома(1.1)

U_B = Z_BI - E_B

3.определяются узловые напряжения по уравнению связи параметров [1]

U_Δ = M_t^-1 U_B

4.на основе полученных данных рассчитываются остальные параметры режима: потоки мощности P, Q; потери ΔР, ΔQ и т.д.

Таким образом, последовательность расчета предполагает решение на первом этапе системы уравнений порядка m, где m – количество ветвей схемы.

Анализ реальных схем показал. Что число ветвей обычно в 1,5 раза больше количества узлов. Поэтому чаще для проведения расчета нормальных режимов используется система уравнений узловых напряжений.

Задание 3.

Для расчетной схемы записать в матричной форме обобщенное уравнение состояния. Перейти к системе алгебраических уравнений относительно неизвестных токов в ветвях.

Дата добавления: 2014-01-06