Момент импульса

Спектр поглощения

Вид спектров светящихся газов зависит от химической природы газа.

Спектр испускания

Вопрос 5. Спектры испускания и спектры поглощения

Если свет от раскаленного твердого тела пропустить через призму, то на экране за призмой получим непрерывный сплошной спектр испускания.

Если источником света является газ или пар, то картина спектра существенно меняется. Наблюдается совокупность ярких линий, разделенных темными промежутками. Такие спектры называются линейчатыми. Примерами линейчатых спектров могут служить спектры натрия, водорода и гелия.

Каждый газ или пар дает свой, характерный только для него спектр. Поэтому спектр светящегося газа позволяет сделать заключение о его химическом составе. Если источником излучения служат молекулы вещества, то наблюдается полосатый спектр.

Все три вида спектров – сплошной, линейчатый и полосатый – являются спектрами испускания.

Помимо спектров испускания существуют спектры поглощения, которые получают следующим образом.

Белый свет от источника пропускают через пары исследуемого вещества и направляют на спектроскоп или иной прибор, предназначенный для исследования спектра.

В этом случае не фоне сплошного спектра видны темные линии, расположенные в определенном порядке. Их число и характер расположения позволяют судить о составе исследуемого вещества.

Например, если на пути лучей находятся пары натрия, на сплошном спектре возникает темная полоса в том месте спектра, где должна была располагаться желтая линия спектра испускания паров натрия.

Рассмотренное явление было объяснено Кирхгофом, показавшим, что атомы данного элемента поглощают те же световые волны, которые они сами испускают.

Чтобы объяснить происхождение спектров, необходимо знать строение атома. Эти вопросы будут рассмотрены в дальнейших лекциях.

Литература:

1. И.И.Наркевич и др. Физика.- Минск: Изд-во “ООО Новое знание”, 2004.

2. Р.И.Грабовский. Курс физики.- СПб.- М.- Краснодар: Изд-во “Лань”, 2006.

3. В.Ф.Дмитриева. Физика.- М.: Издательство “Высшая школа”, 2001.

4. А.Н.Ремизов. Курс физики, электроники и кибернетики.- М.: Изд-во “Высшая школа”, 1982

5. Л.А. Аксенович, Н.Н.Ракина. Физика.- Минск: Издательство “Дизайн ПРО”, 2001.

При сравнении законов вращательного и поступательного движений усматривается аналогия: .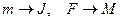

Аналогом импульса является момент импульса. Понятие момента импульса также можно ввести относительно неподвижной точки и относительно неподвижной оси.

Момент импульса материальной точки 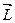относительно неподвижной точки О равен векторному произведению радиуса-вектора 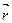, проведенного из полюса О к данной материальной точке, на ее импульс :

.

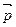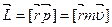Моментом импульса относительно неподвижной оси называется проекция вектора 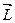на эту ось.

Если материальная точка вращается вокруг неподвижной оси, то её момент импульса относительно этой оси по модулю равен

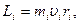
где m_i - масса материальной точки, u _i - её линейная скорость r_i - расстояние до оси вращения.

Т.к. для вращательного движения ,

,

,

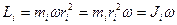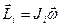где 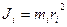- момент инерции материальной точки относительно оси вращения.

Момент импульса твердого тела относительно неподвижной оси равен сумме моментов импульсов всех его точек относительно этой оси:

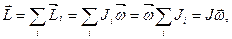
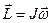, (1)

где 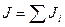- момент инерции тела.

Т.о., момент импульса твердого тела относительно неподвижной оси вращения равен произведению его момента инерции относительно этой оси на угловую скорость и сонаправлен с вектором угловой скорости (рис.1).

Продифференцируем уравнение (1) по времени:

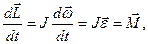
или 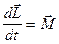. (2)

Уравнение (2) - ещё одна форма основного уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно неподвижной оси вращения равна моменту внешних сил относительно той же оси.

Дата добавления: 2014-01-07