Алфавит. Слова. Алгоритм в алфавите. Вполне эквивалентные алгоритмы

Алфавитом называется всякое непустое множество символов, а сами символы алфавита называются буквами.

Примером алфавита может служить конечное множество символов или, например, русский алфавит.

Словом в данном алфавите А называется всякая конечная последовательность букв алфавита А.

Пустая последовательность букв называется пустым словом и обозначается через Λ.

Если Р обозначает слово аbb и Q обозначает слово bb, то пусть РQ обозначает слово аbbbb, аналогично для любых слов Р и Q запись РQ обозначает слово, полученное из слов Р и Q, если сразу за Р записать слово Q.

Ясно, что для любого слова Р имеем РΛ=ΛР=Р.

Алфавит А называется расширением алфавита В, если 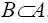. Если алфавит А есть расширение алфавита В, то, очевидно, всякое слово в алфавите В является также словом и в алфавите А, обратное верно не всегда.

Будем говорить, что слово Р входит в слово Q, если Q=R₁PR₂, где R₁и R₂любые, может быть и пустые слова. Слово Р может входить в слово Q несколько раз, первым вхождением будем считать самое левое вхождение.

Под алгоритмом в алфавите А понимается алгоритм, входами и выходами которого являются слова в алфавите А. Таким образом, алгоритм в алфавите А представляет собой потенциально осуществимое преобразование слов в данном алфавите А.

Алгоритмы обозначаются заглавными полужирными буквами (A, B, С,...).

Пусть Р слово в алфавите А. Говорят, что алгоритм A применим к слову Р, если применение его к слову Р приводит через конечное число шагов к некоторому слову Q. При этом слово Q обозначается через A (Р). Если процесс переработки (преобразования) слова Р бесконечен, то считается, что алгоритм не применим к этому слову.

Два алгоритма A и B в одном и том же алфавите С называются вполне эквивалентными в алфавите D , если для любого слова Р в алфавите D либо оба алгоритма не применимы к Р, либо применимы и их результаты совпадают: A (Р) = B (Р). То, что алгоритмы A и B вполне эквивалентны в алфавите D, обозначается следующим образом:

3. Нормальный алгоритм (алгоритм А. А. Маркова)

Опыт изучения и применения математики показывает, что все известные алгоритмы можно разбить на простейшие шаги - элементарные операции. В качестве элементарной операции, на базе которой будут строиться нормальные алгоритмы, выделим подстановку одного слова вместо другого.

Пусть задан алфавит А, не содержащий в качестве букв символов "•" и "→", и пусть Р и Q слова в алфавите А. Тогда выражения Р→Q, P→•Q называются формулами подстановки в алфавите А.

Формула подстановки Р→Q называется простой подстановкой и означает, что вместо Р нужно подставить слово Q и перейти к следующей подстановке.

Формула подстановки Р→•Q называется заключительной подстановкой и означает, что вместо Р нужно подставить Q и закончить процесс преобразования.

Пусть Р→(•)Q означает любую из формул подстановки Р→Q или Р→•Q.

Нормальный алгоритм в алфавите А считается заданным, если задана конечная таблица (схема) формул подстановок слов алфавита А:

n ≥ 1, P_iи Q_i, (1≤i≤n) слова в А, причем согласно этой таблице (схеме) формул подстановок можно осуществлять преобразование слов алфавита А следующим образом.

Пусть R_oслово в алфавите А. Если ни одно из Р₁,Р₂,...,Р_nне входит в R_o, то процесс применения В к R_oзаканчивается и его результатом считается слово R_o. Если хотя бы одно из Р₁,Р₂,...,Р_nвходит в R_o, то отыскиваем самую первую (в порядке следования в таблице) формулу подстановки, такую, что Р_kвходит в R_o. Совершаем подстановку слова Q_kвместо самого левого вхождения слова Р_kв слово R_o. Пусть R₁- результат такой подстановки. Если использованная подстановка Р_k→(•)Q_k- заключительная, то работа алгоритма заканчивается и его результатом считается R₁. Если Р_k→(•)Q_k- простая формула подстановки, то применим к R₁тот же поиск, который был только что применен к R_o, и так далее. В случае, когда через конечное число шагов процесс преобразования закончится, то полученное слово R_iи является результатом. Если же процесс переработки слова R_oбесконечен (никогда не заканчивается), то считаем, что алгоритм не применим к слову R_o.

Нормальный алгоритм над алфавитом А отличается от нормального алгоритма в алфавите А только тем, что в словах Р_iи Q_i(1≤i≤n) могут использоваться не только буквы из алфавита А, но и буквы, не принадлежащие алфавиту А.

Рассмотрим несколько примеров нормальных алгоритмов.

1. Пусть А={a,b,c}. Таблица формул подстановок

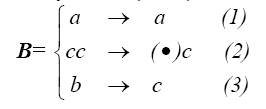
задает некоторый нормальный алгоритм В в алфавите А. Если взять слово R_o=bb, то В преобразует его сначала с помощью подстановки (3) в слово сb, затем, вновь применяя подстановку (3) получим сс. Далее, по заключительной подстановке (2), получим с. Это слово и будет В(R_o).

Если исходное слово R_oбудет содержать букву а, то В не применим к R_o, ибо подстановка (1) будет применяться безостановочно.

2. Пусть А={a,b,c}. Рассмотрим таблицу формул подстановок

Это таблица, очевидно, задает нормальный алгоритм над алфавитом А, ибо β ∉ А. Если взять произвольное слово R_oв А, то к нему сначала подстановки (1),(2) и (3) не применимы, так как слов βа, βb и βс в слове R_oбыть не может. Подставив вместо самого левого пустого слова (Λ) в R_oслово β по (5), имеем βR_o. Если первой в R_oстоит буква а, то применяем подстановку (1), если же первая буква - b, то применяем подстановку (2), а если первая с, то применяем (3) и перемещаем β за первую букву в слове R_o. Повторяя этот процесс столько раз, сколько букв в слове R_o, получим R_oβ. По подстановке (4) окончательно имеем R_oa, т.е. этот алгоритм приписывает к произвольному слову R_oв алфавите А справа от R_oбукву а.

В рассмотренном алгоритме В подстановки (1),(2) и (3) служат для перестановки местами β и а или β и b или β и с, т.е. для перестановки β с любой буквой алфавита А. Тогда можно ввести для нашего алгоритма В более краткую форму записи:

Здесь запись (1*): βx → xβ применена для обозначения подстановок (1)-(3) в В.

Пусть А={a₁,a₂,...,a_n}, P, Q и R слова в алфавите А. Договоримся, что запись вида РхQ → (•)R 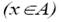обозначает таблицу подстановок:

3. Пусть заданы алфавиты А и В, буква α не входит в А и в В, и пусть a₁,a₂,...,a_k- фиксированные буквы из алфавита А, а Q₁,Q₂,...,Q_k- фиксированные слова в алфавите В. Рассмотрим нормальный алгоритм в алфавите 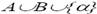, задаваемый таблицей

Этот алгоритм в любом слове Р (алфавита А) все встречающиеся там буквы a₁,a₂,...,a_k- заменяет на слова Q₁,Q₂,...,Q_kсоответственно. Если же в Р букв a₁,a₂,...,a_kнет, то оставляет его без изменения.

Пусть М={1,*}. Любое неотрицательное целое (натуральное) число можно записать (обозначить) в алфавите М словом, состоящим из n+1 букв 1:

число 0 обозначим словом 0=1,

число 1 обозначим словом 1=11,

.............................

число n обозначим словом

Слова 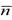будем называть цифрами. Поставим теперь в соответствие всякому вектору (n₁,n₂,...,n_k), где n₁,n₂,...,n_k- натуральные числа, слово в алфавите М, которое обозначим через . Так, например, 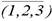(1,2,3 обозначает слово 11*111*1111.

4. Нормальный алгоритм

как легко убедиться, применим только к тем словам в алфавите М, которые суть цифры, и переводит любое слово в 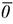, т.е. для любого натурального n. Заметим, что алгоритм A₀ не применим к пустому слову.

5. Нормальный алгоритм

очевидно, тоже применим только к тем словам в алфавите М, которые суть цифры, и преобразует любое слово в слово 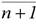, т.е. для любого натурального n. Алгоритм A₁, как и A₀, не применим к пустому слову.

Дата добавления: 2014-01-07