Коды без памяти и алгоритм Хаффмена

Лекция 8. Коды без памяти, коды с памятью и арифметическое кодирование

Простейшими кодами, на основе которых может выполняться сжатие данных, являются коды без памяти. В коде без памяти каждый символ в кодируемом векторе данных заменяется кодовым словом из префиксного множества двоичных последовательностей или слов.

Префиксным множеством двоичных последовательностей S называется конечное множество двоичных последовательностей, таких, что ни одна последовательность в этом множестве не является префиксом, или началом, никакой другой последовательности в S.

Например, множество двоичных слов S1 = {00, 01, 100, 110, 1010, 1011 } является префиксным множеством двоичных последовательностей, поскольку, если проверить любую из 30 возможных комбинаций (w_i w_j) из S1, то видно, что w_i никогда не явится префиксом (или началом) w_j. С другой стороны, множество S2 = { 00, 001, 1110 } не является префиксным множеством двоичных последовательностей, так как последовательность 00 является префиксом (началом) другой последовательности из этого множества - 001.

Таким образом, если необходимо закодировать некоторый вектор данных X = ( x₁, x₂,… x_n) с алфавитом данных A размера k, то кодирование кодом без памяти осуществляется следующим образом:

Ø составляют полный список символов a₁, a₂, a_j...,a_k алфавита A, в котором первым в списке будет стоять наиболее часто встречающийся в алфавите символ, вторым – реже встречающийся и т.д.;

Ø каждому символу a_j назначают кодовое слово w_j из префиксного множества двоичных последовательностей S;

Ø выход кодера получают объединением в одну последовательность всех полученных двоичных слов.

Если S = { w₁, w₂,..., w_k } - префиксное множество, то можно определить некоторый вектор v(S) = (L₁, L₂,..., L_k), состоящий из чисел, являющихся длинами соответствующих префиксных последовательностей (L_i - длина w_i).

Вектор (L₁, L₂,..., L_k), состоящий из неуменьшающихся положительных целых чисел, называется вектором Крафта. Для него справедливо неравенство

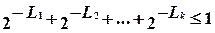. (1)

(неравенство Крафта). Справедливо следующее утверждение: если S - какое-либо префиксное множество, то v(S) - вектор Крафта.

Иными словами, длины двоичных последовательностей в префиксном множестве удовлетворяют неравенству Крафта.

Примеры простейших префиксных множеств и соответствующие им векторы Крафта:

S1 = {0, 10, 11} и v(S1) = (1, 2, 2);

S2 = {0, 10, 110, 111} и v(S2) = (1, 2, 3, 3);

S3 = {0, 10, 110, 1110, 1111} и v(S3) = (1, 2, 3, 4, 4);

S4 = {0, 10, 1100, 1101, 1110, 1111} и v(S4) = (1, 2, 4, 4, 4, 4);

Допустим мы хотим разработать код без памяти для сжатия вектора данных X = (x₁, x₂,… x_n) с алфавитом A размером в k символов. Введем в рассмотрение так называемый вектор частот F = (F₁, F₂,..., F_k), где F_i - количество появлений i -го наиболее часто встречающегося символа из A в X. Закодируем X кодом без памяти, для которого вектор Крафта L = (L₁, L₂,..., L_k).

Тогда длина двоичной кодовой последовательности B(X) на выходе кодера составит

L*F = L₁*F₁ + L₂*F₂ +... + L_k*F_k. (2)

Лучшим кодом без памяти был бы код, для которого длина B(X) - минимальна. Для разработки такого кода нужно найти вектор Крафта L, для которого произведение L*F было бы минимально.

Эффективный способ поиска оптимального вектора Крафта L (т. е. такого L, для которого произведение L*F) минимально) дает алгоритм Хаффмена,. Код, полученный с использованием оптимального L для F, называют кодом Хаффмена.

Дата добавления: 2014-01-07