NP-полные и NP-трудные задачи

Оптимальный раскрой (бумага, стальной прокат, отливка), оптимизация маршрутов в воздушном пространстве, инвестиций, станочного парка;

Размещение обслуживающих центров (телефон, телевидение, срочные службы) для максимального числа клиентов при минимальном числе центров;

NP класс

Наиболее простыми считаются полиномиальные задачи, т.е. задачи класса Р.

Другим, возможно более широким, «сложностным классом» является класс NP. Эта аббревиатура обозначает выражение «разрешимых на недетерминированной машине Тьюринга за полиномиальное время». Оказалось, что многие известные задачи принадлежат к NP классу.

В обычных машинах Тьюринга (их называют детерминированными, чтобы отличать от недетерминированных) новое состояние, в которое машина переходит на очередном шаге, полностью определяется текущим состоянием и тем символом, который обозревает головка на ленте.

В недетерминированных машинах Тьюринга для каждого состояния может быть несколько следующих состояний, в соответствии с функцией перехода. И в каждом следующем состоянии запускается новая копия данной машины Тьюринга.

Недетерминированность лучше всего понять, рассматривая алгоритм, который производит вычисления до тех пор, пока не доходит до места, в котором должен быть сделан выбор из нескольких альтернатив. Детерминированный алгоритм исследовал бы сначала одну альтернативу, а потом вернулся для рассмотрения следующей альтернативы. Недетерминированный алгоритм может исследовать все альтернативы одновременно, «копируя», в сущности, самого себя для каждой альтернативы. Все копии работают независимо. Если копия обнаруживает, что данный путь безрезультатный, то она прекращает выполняться. Если копия находит требуемое решение, она объявляет об этом, и все копии прекращают работать.

Определим NP класс как класс задач, которые можно решить недетерминированными алгоритмами, работающими в течение полиномиального времени.

Чтобы доказать, что некоторая задача принадлежит классу NP, достаточно построить недетерминированный алгоритм (алгоритм недетерминированной машины Тьюринга), который решает эту задачу за полиномиальное время.

Пусть имеем, например, задачу выяснения существования в ориентированном графе гамильтонового цикла, длина которого меньше или равна M.

Рассмотрим следующий алгоритм.

В этом алгоритме рассмотрение каждого варианта, т.е. последовательности соединённых дугами вершин 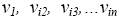требует n шагов. Следовательно, каждая процедура ВЫБОР (иначе каждая копия алгоритма просмотра одного пути) работает не более, чем полиномиальное время, точнее имеет сложность порядка 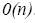. Таким образом, задача выяснения существования в ориентированном графе гамильтонового цикла, длина которого меньше или равна M, является NP задачей.

Детерминированная машина Тьюринга является частным случаем недетерминированной машины Тьюринга (которая не имеет копий), поэтому имеем, что .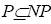

Вопрос о том, будет ли P=NP является открытой проблемой теории сложности. Широко распространено мнение, что 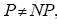, следовательно, .

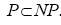Примеры задач из класса NP:

1) выяснение выполнимости формулы логики высказываний, записанной в к.н.ф.;

2) нахождение целочисленных решений системы линейных уравнений;

3) задача распознавания простого числа;

4) выяснение гамильтоновости графа;

5) задача коммивояжёра;

8) составление расписаний, учитывающих определённые условия;

9) оптимальная загрузка ёмкости (рюкзак, поезд, корабль, самолёт) при некоторых условиях;

10) динамическое распределение памяти. Раскроем эту проблему. Пусть заданы А – множество элементов данных, размер 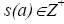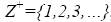, каждого элемента данных 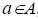, время поступления 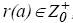, 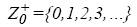и время 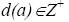окончания работы с элементом данных 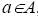, положительное целое число D – размер области памяти. Вопрос. Существует ли для множества элементов данных допустимое распределение памяти? Иначе говоря, существует ли такая функция σ: А→{1,2,3,…}, что для каждого элемента 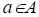интервал

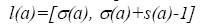
содержится в [1, D], причём для любых 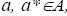, если 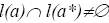, то либо 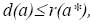, либо .

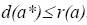В случае, когда размеры всех элементов данных одинаковы, то задача решается за полиномиальное время;

Рассмотрим сводимость задач. Говорят, что задача Z₁ сводится к задаче Z_2, если метод решения задачи Z₂ можно преобразовать в метод решения задачи Z₁. Сводимость называется полиномиальной если указанное преобразование можно осуществить за полиномиальное время.

Если одновременно задача Z₁ полиномиально сводится к задаче Z₂ и Z₂ полиномиально сводится к задаче Z₁, то задачи Z₁ и Z₂ полиномиально эквивалентны.

Задача называется NP-трудной если каждая задача из NP полиномиально сводится к ней.

NP-трудная задача имеет тот смысл, что эта задача не проще, чем «самая трудная в NP».

В классе NP выделяются NP-полные задачи. Задача называется NP-полной, если она входит в NP и каждая задача из NP полиномиально сводится к ней (т.е. является NP-трудной). NP-полные задачи понимаются как самые трудные задачи из класса NP.

Класс NP- полных задач обладает следующими свойствами.

1. Никакую NP-полную задачу нельзя решить никаким известным полиномиальным алгоритмом, несмотря на настойчивые усилия многих блестящих исследователей.

2. Если бы удалось построить полиномиальный алгоритм для какой-нибудь NP-полной задачи, то это бы означало полиномиальную разрешимость каждой NP-полной задачи.

Основываясь на этих двух свойствах, многие высказывают гипотезу, что PNP. Практическое значение понятия NP-полной задачи лежит именно в широко распространенном мнении, что такие задачи по существу труднорешаемы. Следовательно, при их решении в худшем случае потребуется экспоненциальное количество времени и не будет возможности решить на практике такие задачи, за исключением очень малого числа индивидуальных задач.

Первой задачей, для которой было доказано, что она является NP-полной, была проблема о выполнимости (см. задачу 1 в § 4), именно, имеет место следующая теорема.

Теорема 7.1 (теорема Кука). Задача выяснения выполнимости формулы логики высказываний, представленной в к.н.ф., является NP-полной.

Все приведённые ранее примеры NP-задач (задачи 1-12) являются NP-полными задачами. Список NP-полных задач в настоящее время содержит несколько сотен задач и продолжает пополняться. Многие вновь установленные NP-полные задачи печатаются в журнале Journal of Algorithms. В действительности о большей части задач комбинаторной оптимизации известна либо полиномиальная разрешимость, либо NP-полнота, что является ещё одним подтверждением гипотезы P≠NP.

Класс Е.

Считается, что алгоритм имеет полиномиальную временную сложность, если существует полином p(x) такой, что на любом входном слове длины n алгоритм завершает вычисления после выполнения не более чем p(n) операций. Если такого полинома не существует, временная сложность считается экспоненциальной. Таким образом для них число операций возрастает быстрее значений любого полинома.

Кроме этого определения существует и второе определение: алгоритм имеет экспоненциальную временную сложность если его временная сложность имеет порядок не меньше, чем 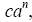, где 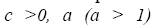- постоянные. Иначе, временная сложность 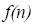является экспоненциальной, если существуют постоянные 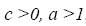, что 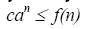для всех, кроме конечного числа значений n.

При первом определении, например задача, имеющая сложность порядка 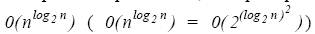будет отнесена к задаче с экспоненциальной временной сложностью, а по второму определению – нет. Отметим, что функция 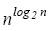хотя и растет быстрее любого полинома, но растёт медленнее, чем, например .

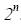Большинство экспоненциальных алгоритмов – это просто варианты полного перебора. Экспоненциальные алгоритмы не считаются «хорошими», в отличие от полиномиальных алгоритмов, которые, как уже указывалось, считаются «хорошими». К экспоненциальным задачам относятся задачи, в которых требуется построить множество всех подмножеств данного множества, все полные подграфы некоторого графа или же все поддеревья некоторого графа.

Некоторые экспоненциальные алгоритмы весьма хорошо зарекомендовали себя на практике. Дело в том, что временная сложность определяется для худшего случая, а многие задачи могут быть не так плохи.

Для решения задачи линейного программирования существует так называемый симплекс-метод (алгоритм), который хотя и экспоненциален в худшем случае – уверено работает на практике для задач достаточно большого размера. Отметим, что для решения задачи линейного программирования Хачиян Л. Г. в 1979 г. предложил алгоритм эллипсоидов, который имеет полиномиальную временную сложность.

Метод ветвей и границ успешно решает задачу о рюкзаке, хотя этот алгоритм имеет экспоненциальную временную сложность.

Примеров экспоненциальных алгоритмов успешно используемых на практике мало. Более того даже для полиномиальных алгоритмов представляют практический интерес алгоритмы сложность которых имеет порядок n2 или n3. Ясно, что алгоритмы со сложностью порядка n100 вряд ли будут практически используемы.

Интересно, что экспоненциальный алгоритм может оказаться при малом размере задачи более быстрым, чем полиномиальный, однако с ростом размера задачи полиномиальный становится более быстрым.

Экспоненциальная сложность задачи имеет следующие аспекты:

-для отыскания решения требуется экспоненциальное время;

-искомое решение может быть настолько велико, что не может быть представлено выражением, длина которого была бы ограничена полиномом от длины входа.

Вторая ситуация возникает, например, если в задаче коммивояжера требуется найти все маршруты длины, не превосходящей заданной величины L. Может оказаться, что имеется экспоненциальное число маршрутов длины не превосходящей L.

Ёмкостная (ленточная) сложность алгоритма

Ёмкостная или ленточная сложность алгоритма характеризует необходимую для вычисления память для хранения исходных данных, промежуточных результатов и окончательного результата. При применении машины Тьюринга как модели вычислений, ёмкостная сложность оценивается длиной части ленты используемой для записи исходных данных и вычислений.

Пусть машина Тьюринга вычисляет значение функции f.

Активной зоной ленты (машины Тьюринга) в данный момент времени t называется связанная часть ленты, содержащая обозреваемую ячейку и все ячейки в которых имеются символы из внешнего алфавита машины. Активной зоной при работе машины Тьюринга на числе n называется объединение всех активных зон за время вычисления.

Определим Sf(x) как длину активной зоны при работе машины Т на числе х, если f(x) определено. В противном случае значение Sf(x) будем считать неопределённым. Функцию Sf(x) назовём ленточной сложностью.

Отметим, что в настоящее время уделяется существенно больше внимания временным характеристикам и значительно меньше ёмкостным, хотя эта характеристика тоже существенна при использовании ЭВМ с ограниченной памятью.

Для задач вводятся понятия задач с полиномиальной потребной памятью, с NP-потребной памятью и т.д.

Имеет место следующая теорема:

Теорема. Для ленточной (ёмкостной) характеристики сложности вычисления функции f имеет место оценка

где 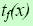-временная сложность вычисления f(x).

Доказательство. В начальный момент на ленте машины Тьюринга записано число х (в унарной системе), следовательно, занято х+1 клеток ленты. На каждом такте (шаге) активной становится не более одной новой клетки, поэтому получим указанную оценку для Sf (x).

Эта теорема показывает, что если известна временная сложность, то можно оценить сверху ленточную сложность.

Интересно, что нет пределов сложности вычислений. Можно доказать, что какую бы сложную задачу не взять, то существует ещё более сложная задача.

Дата добавления: 2014-01-07