Нормальное распределение

Нормальным называют распределение вероятностей непрерывной случайной величины, дифференциальная функция которою определяется формулой:

f(x)=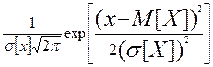 (2/36)

Видно, что дифференциальная функция (плотность вероятности) определяется двумя параметрами (числовыми характеристиками): математическим ожиданием М[Х] и средним квадратическим отклонением σ[Х] (рис.2.9).

f(x)

σ₁

σ₂>σ₁

0 M[X] x

График нормального распределения дифференциальной функции

Площадь под кривой f(x) равна единице, то есть

,

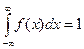так как нормальное распределение применимо для непрерывных величин, изменяющихся во всем диапазоне действительных чисел (от - ∞до ∞).

При M[X]=0 и σ[X]=1 нормальная кривая называется нормированной (рис.2.10), φ(t)

M[X]=0

σ[X]=1

0 t

рис.2.10 Нормированная кривая нормального распределения

Тогда 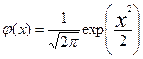(2.37)

Очевидно соотношение:

(2.38)

Значения функции φ(х) интеграла (2.38) в пределах от 0 до текущего значения х табулированы.

Если случайная величина принимает только положительные значения (например, время наработки до отказа, время реакции оператора на отказ объекта), то

(2.39)

Рассмотрим задачу определения вероятности того, что случайная величина – время t наработки до отказа примет значение, принадлежащее интервалу (t₁, t₂), то есть

p(t₁< t < t₂)=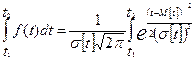 (2.40)

Введем обозначение: z= - 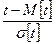, тогда

Dt=σ[t]dz

Новыми пределами интегрирования будут:

При t=t₁

Z₁= - ;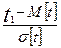

При t=t₂

Z₂= - .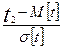

В результате введения z переходим от функции f(t) к функции φ(t), которая представляет собой кривую нормированного нормального распределения (рис.2.11):

f(t) φ(z)

замена

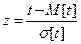
0 t₁ M[t] t₂ z₁ 0 z₂

рис.2.11 Применение нормированного нормального распределения для решения практических задач

Тогда p(t₁<t<t₂)=.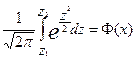

Выражение вида 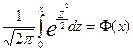(2.41)

называется функцией Лапласа; ее значения в зависимости от х приведены в специальных таблицах.

В нашем случае

P(t₁<t<t₂)=Ф(z₁) - Ф(z₂)=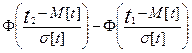. (2.42)

Пример. Время наработки до отказа распределено по нормальному закону и имеет параметры: М[t]=300ч.; σ[X]=50ч.

Требуется определить вероятность того, что объект не откажет в течении времени, лежащего в интервале (200ч., 400ч.).

Решение.

P(200<t<400)=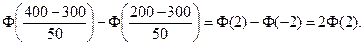

Из таблиц получаем Ф(2)=0,4772.

Тогда р(200<t<400)=2*0,4772=0,9544.

Рассмотрим одно важное понятие, присущее нормальному распределению, так называемое «правило трех сигм».

Определим вероятности того, что случайная величина Х не выйдет из интервала, ограниченного утроенным средним квадратическим отклонением6

P[(M[X]-3σ[X])<X<(M[X]+3σ[X])]=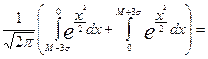

=

=

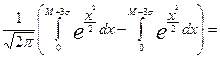
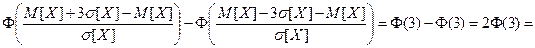
=2*0,49865=0,9973

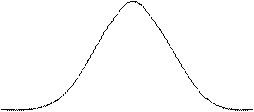
Это означает, что вероятность того, что отклонение случайной величины от математического ожидания не выйдет за пределы утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение («три сигмы»), очень мала и равна 0,0027. Следовательно, можно с достаточной для практики точностью считать, что все возможные значения случайной величины, распределенной по нормальному закону, лежат в пределах «трех сигм» (рис.2.12).

f(x)

0 M[x]

M[x]-3σ[x] M[x]+3σ[x]

Рис.2.12 Правило «трех сигм»

Если случайная величина может принимать только положительные значения, отличные от нуля (например, наработка до отказа), то распределение ее вероятности может быть усеченным нормальным.

Дата добавления: 2014-01-07