Метод Алми имеет два преимущества

1. Он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов.

2. При относительно небольшом количестве переменных в (6) (обычно выбирают k = 2 или k = 3), которое не приводит к потере значительного числа степеней свободы, с помощью метода Алмон можно построить модели с распределенным лагом любой длины.

3. Модель Койка. Рассмотренные модели были построены в предположении конечной длины лага l.

Предположим, что для описания некоторого процесса используется модель с бесконечным лагом вида

y_t = a + b₀x_t + b₁x_t-1 + b₂x_t-2 + … + ε_t. (7)

Параметры такой модели обычным МНК определить нельзя из-за бесконечного числа факторов. Однако, приняв определенные допущения относительно структуры лага, оценки ее параметров все же можно получить. Эти допущения состоят в наличии геометрической структуры лага, т.е. такой структуры, когда воздействия лаговых значений фактора на результат уменьшаются с увеличением величины лага в геометрической прогрессии.

Впервые такой подход к оценке параметров моделей с распределенным лагом был предложен Л.М. Койком. Койк предположил, что существует некоторый постоянный темп λ (0 < λ < 1) уменьшения во времени лаговых воздействий фактора на результат. Если, например, в период t результат изменялся под воздействием изменения фактора в этот же период времени на b₀ ед., то под воздействием изменения фактора, имевшего место в период

(t – 1), результат изменится на b₀λ ед.; в период (t – 2) – на b₀λ² ед., и т.д. Для некоторого периода (t – l) это изменение результата составит b₀λ^l ед. В более общем виде можно записать:

b_j = b₀ λ; j = 0, 1, 2, …, 0<λ<1 (8)

Ограничение на значения λ > 0 обеспечивает одинаковые знаки для всех коэффициентов b_j > 0, а ограничение b_j < 1 означает, что с увеличением лага значения параметров модели (7) убывают в геометрической прогрессии. Чем ближе λ к нулю, тем выше темп снижения воздействия фактора на результат во времени и тем большая доля воздействия на результат приходится на текущие значения фактора х_t.

Выразим с помощью (8) все коэффициенты b_j в модели (7) через b₀ и λ:

y_t = a + b₀x_t + b₀ λx_t-1 + b₀ λ²x_t-2 + … + ε_t (9)

Тогда для периода (t – 1) модель (9) можно записать следующим образом:

y_t-1 = a + b₀x_t-1 + b₀λx_t-2 + b₀λ²x^t-3 + … + ε_t-1 (10)

Умножим обе части (10) на λ:

λy_t-1 =λ a + b₀ λx_t-1 + b₀λ² x_t-2 + b₀λ³ x^t-3 + … +λ ε_t-1 (11)

Вычтем найденное соотношение (11) из соотношения (9):

y_t – λy_t-1 = a – λa + b₀ x_t + ε_t-1 - λ ε_t-1 (12)

Преобразовав (12), получим модель Койка:

y_t = a(1 – λ) + b₀ x_t + (1 – λ)y_t-1 + u_t, (13)

где u_t = ε_t – λε_t-1.

Полученная модель есть модель двухфакторной линейной регрессии (точнее – авторегрессии). Определив ее параметры, мы найдем λ и оценки параметров а и b₀ исходной модели. Далее с помощью соотношений (8) можно определить параметры b₁, b₂, … модели (7). Отметим, что применение обычного МНК к оценке параметров модели (13) приведет к получению смещенных оценок ее параметров ввиду наличия в этой модели в качестве фактора лаговой результативной переменной y_t-1.

Описанный алгоритм получил название преобразования Койка. Это преобразование позволяет перейти от модели с бесконечными распределенными лагами к модели авторегрессии, содержащей две независимые переменные: x_t и y_t-1.

Несмотря на бесконечное число лаговых переменных в модели (7), геометрическая структура лага позволяет определить величины среднего и медианного лагов в модели Койка. Поскольку сумма коэффициентов регрессии в модели (7) есть сумма геометрической прогрессии, т.е.

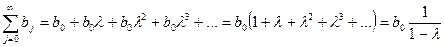, (14)

то средний лаг определяется как

(15)

Нетрудно заметить, что при λ = 0,5 средний лаг 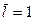, а при l < 0,5 средний лаг , т.е. воздействие фактора на результат в среднем занимает менее одного периода времени. Величину (1 – λ) интерпретируют обычно как скорость, с которой происходит адаптация результата во времени к изменению факторного признака. Для расчета медианного лага необходимо выполнение следующего условия:

(16)

Поэтому медианный лаг в модели Койка равен

.

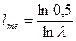Дата добавления: 2014-01-07