Плотности вероятности

Определение характеристик функции

Важнейшими характеристиками распределения вероятностей являются первый, второй, третий и четвертый моменты распределения.

Первый момент m представляет собой математическое ожидание случайной величины x_i или центр тяжести функции плотности вероятности f(x) относительно x = 0. Первый момент называют также средним значением. Этот момент определяется для непрерывного распределения

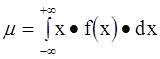(4-5)

а для дискретного распределения

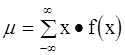(4-6)

Второй момент s² характеризует разброс случайно величины относительно математического ожидания. Его называют также моментом инерции или дисперсией. Квадратный корень из дисперсии представляет собой среднюю квадратическую ошибку или стандартное отклонение s. Дисперсия записывается в виде

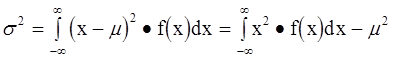(4-7)

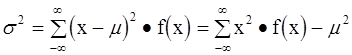или (4-8)

Третий момент характеризует асимметрию распределения случайной величины относительно математического ожидания.

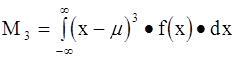(4-9)

- для непрерывного распределения и

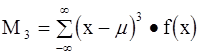(4-10)

- для дискретного распределения.

Если М₃>0, то пик графика функции смещен влево, если М₃<0, то - вправо. Если М₃=0, то график функции симметричен относительно x=m (рис. 4.3.).

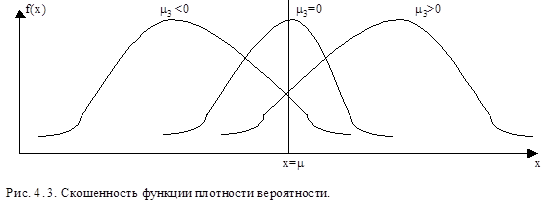
Четвертый момент является мерой эксцесса, характеризующего пологость или заостренность кривой. Он записывается для непрерывного распределения

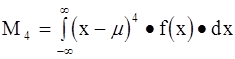(4-11)

а для дискретного распределения

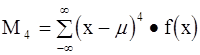(4-12)

Если s = 1 и М₄>3, то график функции имеет заостренный характер, если М₄=3, то график функции имеет среднюю заостренность, а если М₄<3, то кривая плоская (рис. 4.4.).

Таким образом, функция плотности распределения вероятностей характеризуется средним значением, дисперсией или стандартным отклонением, асимметрией и эксцессом. Дополнительными ее характеристиками могут быть мода и медиана.

Модой называется число на оси абсцисс, соответствующее наибольшей плотности вероятности.

Медиана представляет собой число на оси абсцисс, слева и справа от которого случайная величина может находиться с вероятностью 1/2.

Имеются несколько типов распределения вероятностей, применяемых при моделировании на вычислительных машинах. К ним относятся непрерывные распределения: равномерное, нормальное (гаусово), экспоненциальное, логнормальное, x², Стьюдента (или t), F и др.; и дискретные: биномиальное (Бернулли), Пуассона и т.д.

5.1. Основные законы распределения вероятностей

Дата добавления: 2014-01-07