Двойной интеграл

Квадратичная функция.

Линейная функция.

П.6. Основные числовые функции и их графики

Пример 6.12.

Основными элементарными функциями называются следующие: степенная функция, где a любое действительное число; показательная функция, где а >0, a ≠1; логарифмическая функция, где а >0, a ≠1; тригонометрические функции y = sin x, y = cos x,

y = tg x, y = ctg x; обратные тригонометрические функции y = arcsin x, y = arccos x, y = arctg x, y = arcctg x.

Степенная функция. Область определения степенной функции зависит от показателя a. Эта функция при любом a определена в интервале 0 < х < +¥, то есть для всех положительных значений х. При a натуральном областью определения является вся числовая ось. Множеством значений функции будет интервал 0 < у < +¥ при a четном и промежуток –¥ < у < +¥ при a нечетном (рис. 1).

Рис. 1

Показательная функция. Областью определения показательной функции является вся числовая ось, то есть промежуток (–¥; + ¥), а множеством значений функции - промежуток (0; + ¥) (рис. 2).

Рис. 2

Логарифмическая функция. Областью определения логарифмической функции является промежуток, а множеством значений функции - промежуток (рис. 3).

Рис. 3

Тригонометрические функции. Областью определения функций y = sin x и y = cos x является промежуток, а множеством значений функций –– отрезок [–1; 1] (рис. 4 и 5).

Рис. 4 Рис. 5

Функция определена на всей числовой оси, кроме точек, т.е. область определения этой функции есть совокупность интервалов

.

Функция определена на всей числовой оси, кроме точек, т.е. область определения этой функции состоит из интервалов

.

Множеством значений функций и является промежуток (рис. 6 и 7).

Рис. 6 Рис. 7

Обратные тригонометрические функции. Областью определения функций y = arcsin x и

y = arccos x является отрезок [– 1; 1]. Множеством значений функции y = arcsin x является отрезок, а функции y = arccos x –– отрезок (рис. 8 и 9).

Рис. 8 Рис. 9

Областью определения функций y = arctg x и y = arcсtg x является промежуток. Множеством значений функции y = arctg x будет интервал, а функции y = arcсtg x –– интервал (рис. 10 и 11).

Рис. 10 Рис. 11

16.1.1. Определение двойного интеграла. Теорема существования двойного интеграла. Пусть на плоскости Oxy задана ограниченная замкнутая область D с кусочно-гладкой границей, и пусть на области D определена функция .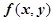

Разобьём область D произвольным образом на 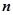подобластей 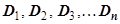(не имеющих общих внутренних точек). Символом будем обозначать площадь области ; символом здесь и дальше будет обозначаться наибольшее расстояние между двумя точками, принадлежащими области D:

;

символом 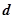обозначим наибольший из диаметров областей : .

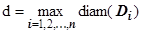В каждой из подобластей 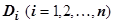выберем произвольную точку , вычислим в этой точке значение функции 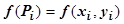, и составим интегральную сумму .

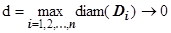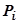Если существует предел последовательности интегральных сумм при , не зависящий ни от способа разбиения области D на подобласти , ни от выбора точек , то функция 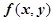называется интегрируемой по области D, а значение этого предела называется двойным интегралом от функции 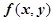по области D и обозначается .

Если расписать значение 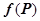через координаты точки , и представить как , получим другое обозначение двойного интеграла: . Итак, кратко, .

Теорема существования двойного интеграла. Если подынтегральная функция 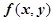непрерывна на области D, то она интегрируема по этой области.

16.1.2. Геометрический смысл двойного интеграла. Геометрический смысл каждого слагаемого интегральной суммы: если 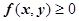, то - объём прямого цилиндра с основанием высоты ; вся интегральная сумма - сумма объёмов таких цилиндров, т.е. объём некоторого ступенчатого тела (высота ступеньки, расположенной над подобластью , равна ). Когда 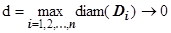, это ступенчатое тело становится всё ближе к изображенному на рисунке телу, ограниченному снизу областью 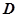, сверху - поверхностью , с цилиндрической боковой поверхностью, направляющей которой является граница области 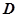, а образующие параллельны оси 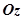. Двойной интеграл равен объёму этого тела.

Дата добавления: 2014-01-07