Криволинейный интеграл первого рода (по длине дуги)

16.3.2.1. Определение криволинейного интеграла первого рода. Пусть в пространстве переменных x,y,z задана кусочно-гладкая кривая 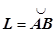, на которой определена функция f (x, y, z).Разобьём кривую точками 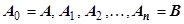на 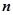частей, на каждой из дуг 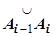выберем произвольную точку 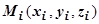, найдём 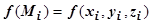и длину 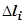дуги 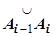, и составим интегральную сумму 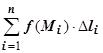. Если существует предел последовательности интегральных сумм при 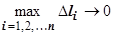, не зависящий ни от способа разбиения кривой на дуги 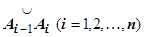, ни от выбора точек 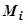, то функция f (x, y, z) называется интегрируемой по кривой 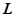, а значение этого предела называется криволинейным интегралом первого рода, или криволинейным интегралом по длине дуги от функции f (x, y, z) по кривой 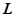, и обозначается 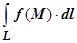(или ).

Теорема существования. Если функция f (x, y, z) непрерывна на кусочно-гладкой кривой 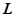, то она интегрируема по этой кривой.

Случай замкнутой кривой. В этом случае в качестве начальной и конечной точки можно взять произвольную точку кривой. Замкнутую кривую в дальнейшем будем называть контуром и обозначать буквой С. То, что кривая, по которой вычисляется интеграл, замкнута, принято обозначать кружочком на знаке интеграла: .

16.3.2.2. Свойства криволинейного интеграла первого рода. Для этого интеграла имеют место все шесть свойств, справедливых для определённого, двойного, тройного интеграла, от линейности до теоремы о среднем. Сформулировать и доказать их самостоятельно. Однако для этого интеграла справедливо и седьмое, персональное свойство:

Независимость криволинейного интеграла первого рода от направления прохождения кривой: .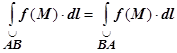

Доказательство. Интегральные суммы для интегралов, стоящих в правой и левой частях этого равенства, при любом разбиении кривой и выборе точек 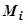совпадают (всегда длина дуги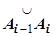 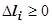), поэтому равны их пределы при .

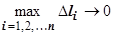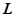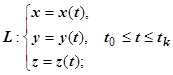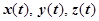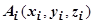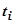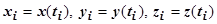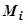16.3.2.3. Вычисление криволинейного интеграла первого рода. Примеры. Пусть кривая задана параметрическими уравнениями , где - непрерывно дифференцируемые функции, и пусть точкам , которые задают разбиение кривой, соответствуют значения параметра , т.е. . Тогда (см. раздел 13.3. Вычисление длин кривых) . По теореме о среднем, существует точка такая, что . Выберем точки , получающиеся при этом значении параметра: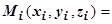 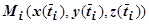. Тогда интегральная сумма для криволинейного интеграла будет равна интегральной сумме для определенного интеграла . Так как 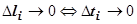, то, переходя к пределу при 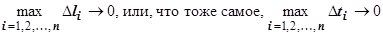в равенстве , получим

.

Таким образом, вычисление криволинейного интеграла первого рода сводится к вычислению определённого интеграла по параметру. Если кривая задана параметрически, то этот переход не вызывает трудностей; если дано качественное словесное описание кривой, то основной трудностью может быть введение параметра на кривой. Ещё раз подчеркнём, что интегрирование всегда ведётся в сторону возрастания параметра.

Примеры. 1. Вычислить , где 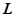- один виток спирали

Здесь переход к определённому интегралу проблем не вызывает: находим , и .

2. Вычислить тот же интеграл по отрезку прямой, соединяющей точки и .

Здесь прямого параметрического задания кривой нет, поэтому на АВ необходимо ввести параметр. Параметрические уравнения прямой имеют вид где 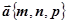- направляющий вектор, - точка прямой. В качестве точки берем точку , в качестве направляющего вектора - вектор : . Легко видеть, что точка соответствует значению , точка - значению , поэтому .

3. Найти, где 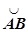- часть сечения цилиндра плоскостью z = x +1, лежащая в первом октанте.

Решение: Параметрические уравнения окружности - направляющей цилиндра имеют вид x =2cosj, y =2sinj, и так как z=x +1, то z = 2cosj+1. Итак,

поэтому

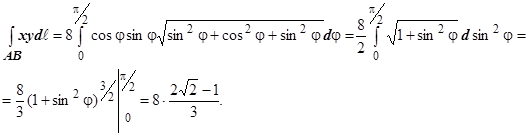
16.3.2.3.1. Вычисление криволинейного интеграла первого рода. Плоский случай. Если кривая лежит на какой-либо координатной плоскости, например, плоскости Оху, и задаётся функцией , то, рассматривая х как параметр, получаем следующую формулу для вычисления интеграла: . Аналогично, если кривая задаётся уравнением , то .

Пример. Вычислить , где 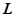- четверть окружности , лежащая в четвёртом квадранте.

Решение. 1. Рассматривая х как параметр, получаем , поэтому

.

2. Если за параметр взять переменную у, то и .

3. Естественно, можно взять обычные параметрические уравнения окружности : .

Если кривая задана в полярных координатах , то , и .

Дата добавления: 2014-01-07