Криволинейный интеграл второго рода (по координатам)

Механические приложения криволинейного интеграла 1-го рода.

16.3.2.4.1. Масса m материальной кривой 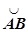с плотностью m(x, y, z) вычисляется по формуле .

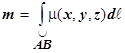Пример. Найти массу четверти лемнискаты 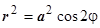, если плотность выражается формулой m(x, y)=.

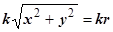Решение: 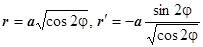, поэтому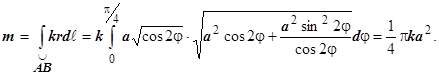

16.3.2.4.2. Статические моменты и координаты центра масс. Пусть плоская материальная кривая 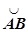имеет плотность m(x, y). Статический момент относительно оси Ox определяется по формуле 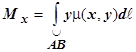, относительно оси Oy: .

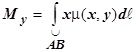Аналогично, статические моменты пространственной кривой относительно координатных плоскостей вычисляются по формулам

, ,

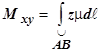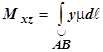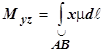
Координаты центра масс могут быть найдены по формулам

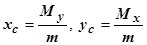- для плоской кривой;

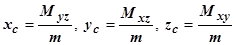- для пространственной кривой, где m - масса кривой.

Пример. Найти центр масс четверти однородной окружности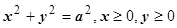

Решение: Можно считать, что m=1. Тогда масса кривой равна ее длине 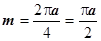. Статический момент 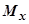равен

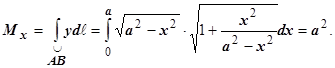
Из соображений симметрии 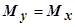, поэтому координаты центра масс равны

.

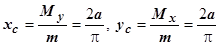16.3.2.4.3. Моменты инерции. Моменты инерции плоской кривой 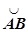с плотностью m относительно координатных осей вычисляются по формулам

,

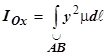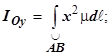
моменты инерции относительно начала координат

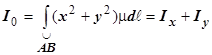
В случае пространственной кривой моменты инерции относительно координатных осей и начала координат определяются по формулам

, , ,

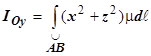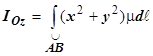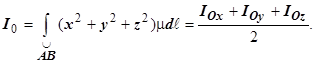
Пример. Найти момент инерции относительно оси Oz однородной винтовой линии (m=1) x = a cos t, y = a sin t, z = at; 0 £ t £ 2p

Решение: .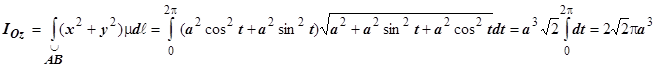

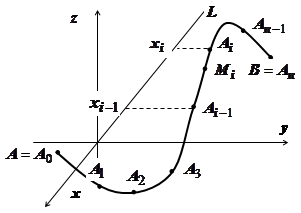16.3.3.1. Определение криволинейного интеграла второго рода. Пусть в пространстве Oxyz дана кусочно-гладкая кривая 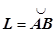, на которой определена функция 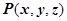. Разобьём кривую точками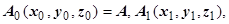 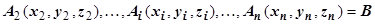на 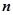частей, на каждой из дуг 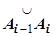выберем произвольную точку 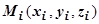, найдём 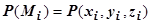и проекцию 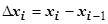дуги 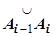на ось Ох, и составим интегральную сумму 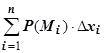. Если существует предел последовательности интегральных сумм при 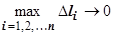, не зависящий ни от способа разбиения кривой на дуги 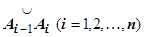, ни от выбора точек 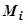, то функция Р (x, y, z) называется интегрируемой по кривой 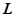, а значение этого предела называется криволинейным интегралом второго рода, или криволинейным интегралом по координате х от функции Р (x, y, z) по кривой 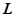, и обозначается 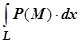(или ).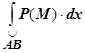

Теорема существования. Если функция Р (x, y, z) непрерывна на кривой 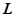, то она интегрируема по этой кривой.

Если на кривой 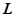, вместе с функцией Р (x, y, z), заданы функции Q (x, y, z) и R (x, y, z), то, аналогично интегралу 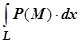, определяются интегралы и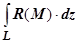. В приложениях рассматривается сумма этих интегралов, которая обозначается 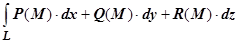и также называется криволинейным интегралом второго рода. Если кривая, по которой ведётся интегрирование, является контуром (т.е. замкнута), то, как и для криволинейного интеграла по длине дуги, в качестве начальной (и совпадающей с ней конечной) точки можно взять любую точку кривой.

16.3.3.2. Свойства криволинейного интеграла второго рода. Для этого интеграла существенны следующие свойства:

16.3.3.2.1. Линейность. Если функции 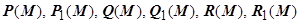интегрируемы по кривой 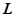(каждая по своей координате, то по этой кривой интегрируемы функци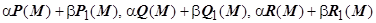и , и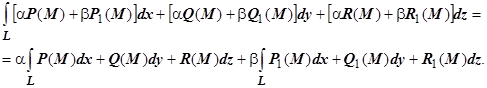

16.3.3.2.2. Аддитивность. Если кривая 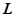разбита на две част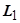и и , не имеющие общих внутренних точек, то .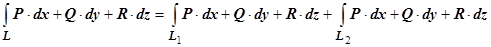

Доказательство этих свойств такое же, как и для других типов интегралов; воспроизвести их самостоятельно. Персональное свойство криволинейного интеграла по координатам:

16.3.3.2.3. Изменение знака криволинейного интеграла второго рода при изменении направления прохождения кривой: .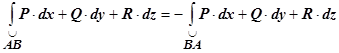

Доказательство очевидно: при изменении направления прохождения кривой меняет знак каждая проекция 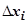, следовательно, меняет знак интегральная сумма, следовательно, меняет знак предел последовательности интегральных сумм.

16.3.3.3. Вычисление криволинейного интеграла второго рода. Примеры. Пусть кривая 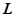задана параметрическими уравнениями 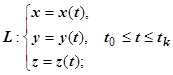, где 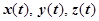- непрерывно дифференцируемые функции, и пусть точкам 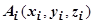, которые задают разбиение кривой, соответствуют значения параметра 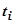, т.е. 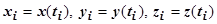. Тогда по теореме Лагранжа существуют такие точки 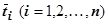, что 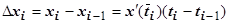. Выберем точки 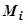, получающиеся при этих значениях параметра: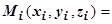 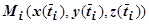. Тогда интегральная сумма для криволинейного интеграла 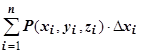будет равна интегральной сумме для определенного интеграла 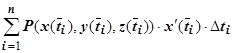. Так как 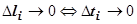, то, переходя к пределу при 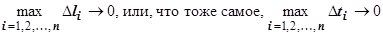в равенстве 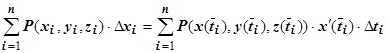, получим

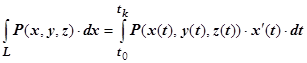. Аналогично доказываются формулы для интегралов по другим координатам. Окончательно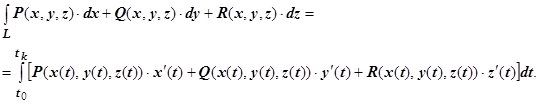

Таким образом, вычисление криволинейного интеграла второго рода ни чем не отличается от вычисления интеграла первого и сводится к интегрированию по параметру. Направление интегрирования определяется условиями задачи.

Примеры. 1. Найти 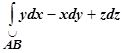, где 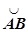- виток винтовой линии x = a ×cos t, y = a ×sin t, z = a × t, 0 £ t £ 2p.

Решение: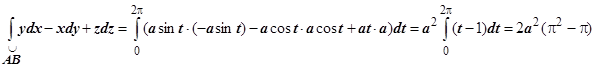

Пусть плоская кривая задана в декартовой системе координат уравнением y = y (x), A (a, y (a)), B (b, y (b)). Тогда

Дата добавления: 2014-01-07